Graph Clustering Coefficient
Local Clustering Coefficient
$$ c_u = \frac{ \lvert (v_1,v_2)\in \mathcal E: v_1, v_2 \in \mathcal N(u) \rvert}{ \color{red}{d_n \choose 2} }, $$
where $\color{red}{d_n \choose 2}$ means all the possible combinations of neighbor nodes, and $\mathcal N(u)$ is the set of nodes that are neighbor to $u$.
Closed Triangles
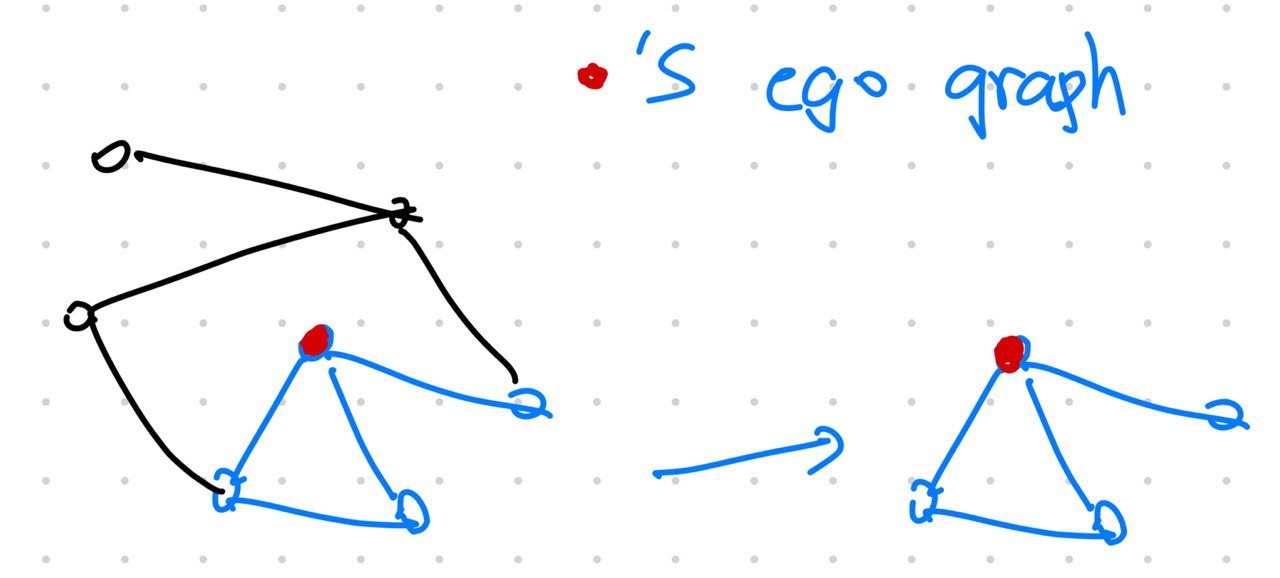
Counting the closed triangles of the ego graph of a node and normalize it by the total possible number of triangles is also a measure of clustering coefficients.
- If the ego graph of $u$ is fully connected, we have $c_u=1$;
- If the ego graph of $u$ is a star, we have $c_u=0$.
This concept can be generalized from triangles to any type of motifs.
Planted:
by L Ma;
References:
Dynamic Backlinks to
cards/graph/graph-local-clustering-coefficient:cards/graph/graph-local-clustering-coefficient Links to:L Ma (2021). 'Graph Clustering Coefficient', Datumorphism, 09 April. Available at: https://datumorphism.leima.is/cards/graph/graph-local-clustering-coefficient/.