Graph Clustering Coefficient

Local Clustering Coefficient

$$ c_u = \frac{ \lvert (v_1,v_2)\in \mathcal E: v_1, v_2 \in \mathcal N(u) \rvert}{ \color{red}{d_n \choose 2} }, $$

where $\color{red}{d_n \choose 2}$ means all the possible combinations of neighbor nodes, and $\mathcal N(u)$ is the set of nodes that are neighbor to $u$.

Closed Triangles

Ego Graph

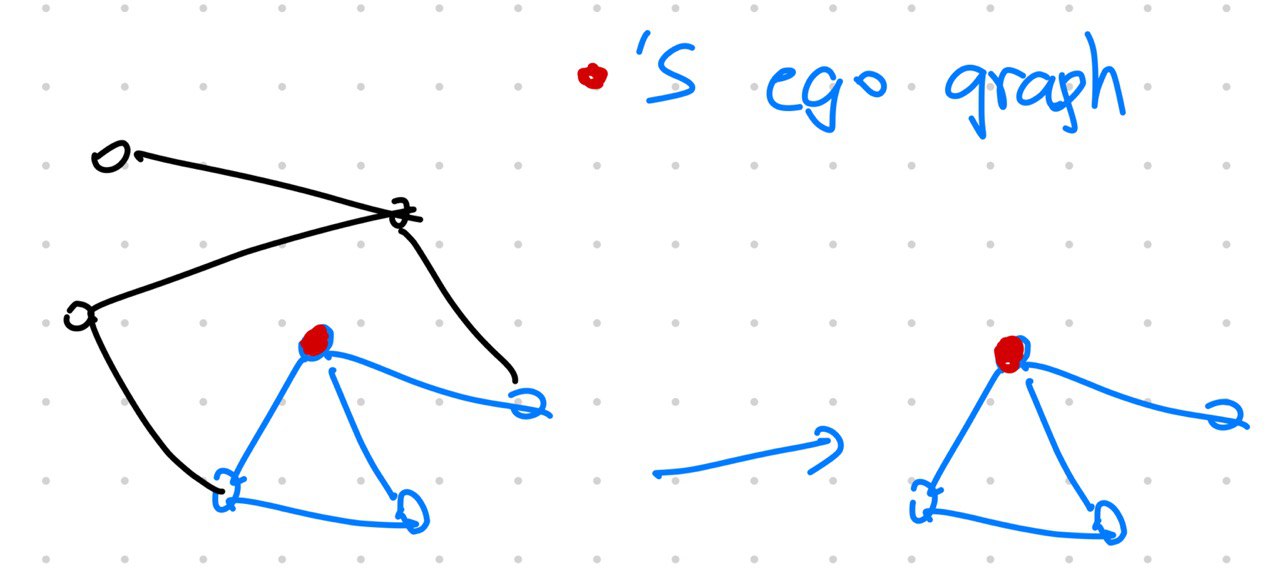
Counting the closed triangles of the ego graph of a node and normalize it by the total possible number of triangles is also a measure of clustering coefficients.

• If the ego graph of $u$ is fully connected, we have $c_u=1$;
• If the ego graph of $u$ is a star, we have $c_u=0$.

This concept can be generalized from triangles to any type of motifs.