Generative Model: Normalizing Flow
Normalizing flow is a method to convert a complicated distribution $p(x)$ to a simpler distribution $\tilde p(z)$ by building up a map $z=f(y)$ for the variable $x$ to $z$. The relations between the two distributions is established using the conservation law for distributions, $\int p(x) \mathrm d x = \int \tilde p (z) \mathrm d z = 1$. One could imagine that changing the variable also brings in the Jacobian.
![Liu X, Zhang F, Hou Z, Wang Z, Mian L, Zhang J, et al. Self-supervised Learning: Generative or Contrastive. arXiv [cs.LG]. 2020. Available: http://arxiv.org/abs/2006.08218](../assets/generative-flow/generative-flow-illustration.png)
Liu X, Zhang F, Hou Z, Wang Z, Mian L, Zhang J, et al. Self-supervised Learning: Generative or Contrastive. arXiv [cs.LG]. 2020. Available: http://arxiv.org/abs/2006.08218
Architecture
For a probability density $p(x)$ and a transformation of coordinate $x=g(z)$ or $z=f(x)$, the density can be expressed using the coordinate transformations, i.e.,1
$$ \begin{align} p(x) &= \tilde p (f(x)) \lvert \operatorname{det} \operatorname{D} g(f(x)) \rvert^{-1} \\ &= \tilde p(f(x)) \lvert \operatorname{det}\operatorname{D} f(x) \rvert \end{align} $$
where the Jacobian is
$$ \operatorname{D} g(z) \to \frac{\partial }{\partial z} g. $$
The operation $g _ { * }\circ \tilde p(z)$ is the pushforward of $\tilde p(z)$. The operation $g _ { * }$ will pushforward simple distribution $\tilde p(z)$ to a more complex distribution $p(x)$.
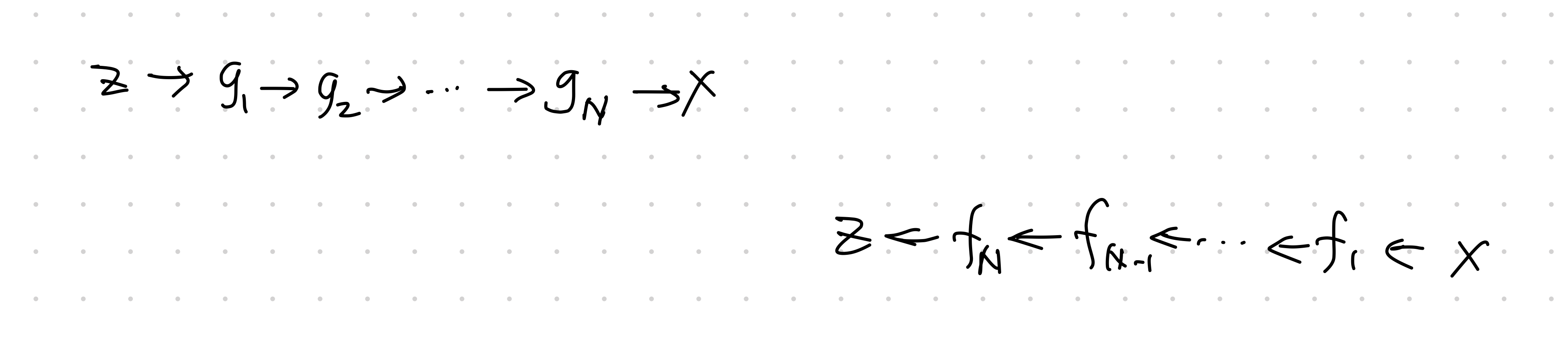
- The generative direction: sample $z$ from distribution $\tilde p(z)$, apply transformation $g(z)$;
- The normalizing direction: “simplify” $p(x)$ to some simple distribution $\tilde p(z)$.
The key to the flow model is the chaining of the transformations
$$ \operatorname{det} \operatorname{D} f(x) = \Pi_{i=1}^N \operatorname{det} \operatorname{D} f_i (x_i) $$
where
$$ \begin{align} x_i &= g_i \circ \cdots \circ g_1 (z)\\ &= f_{i+1} \circ \cdots \circ f_N (x). \end{align} $$
Applications
Normalizing flow is good at estimating densities, fast.1
Variational Inference
One interesting use case of the normalizing flow model is variational inference. We reiterate section 2.2.2 of Liu2020 here.1
In an inference problem, $p(z\vert x)$, which is used to infer $z$ from $x$.
p(z\vert x) = \frac{p(x, z)}{p(x)}.
For example, we have an observable $x$ and a latent space $z$, we would like to find a good latent space for the observable $x$. However, $p(x)$ is something we don’t really know. We would like to use some simpler quantities to help us inferring $z$ from $x$ or generating $x$ from $z$.
Now we introduce a simple distribution $q(z\vert x)$. We want to make sure this $q(z\vert x)$ …
- The variational inference problem: $\ln p(x) = \int \ln p(x, y) dy = $:
- $x$ is the observable;
- $y$ is the latent variable.
- Introduce an approximation of the posterior $q(y\vert x, \theta)$, see
wiki/machine-learning/generative-models/flow Links to:L Ma (2021). 'Generative Model: Normalizing Flow', Datumorphism, 08 April. Available at: https://datumorphism.leima.is/wiki/machine-learning/generative-models/flow/.