Generative Model: Autoregressive Model

#Self-supervised Learning #Generative Model #Autoregressive Model #Basics

An autoregressive (AR) model is autoregressive,

$$ \begin{equation} \log p_\theta (x) = \sum_{t=1}^T \log p_\theta ( x_{t} \mid {x_{<t}} ). \end{equation} $$

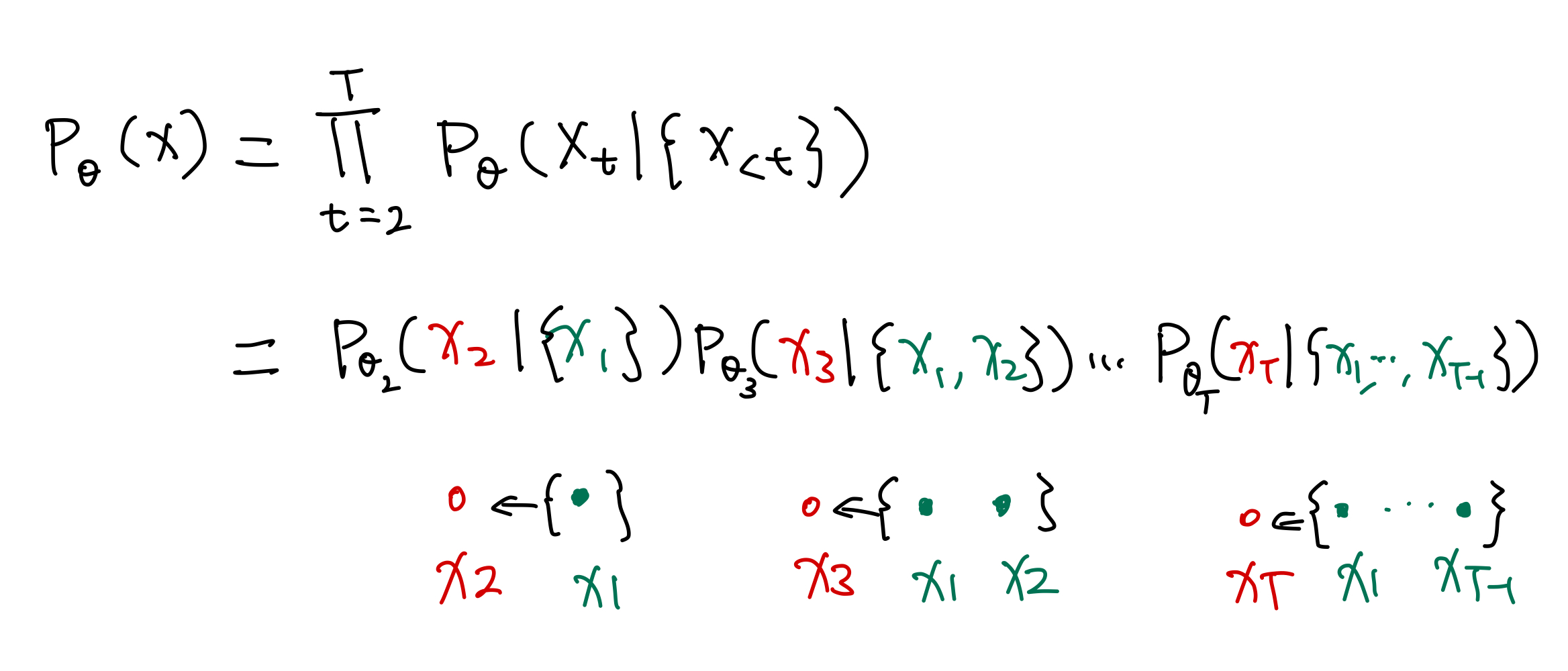
In the above example, the likelihood is modeled as

$$ \begin{align} p_\theta (x) &= \Pi_{t=1}^T p_\theta (x_t \mid x_{1:t-1}) \\ &= p_\theta(x_2 \mid x_{1:1}) p_\theta(x_3 \mid x_{1:2}) \cdots p_\theta(x_T \mid x_{1:T-1}) \end{align} $$

Taking the log of it

$$ \ln p_\theta (x) = \sum_{t=1}^T \ln p_\theta (x_t \mid x_{1:t-1}) $$

Notations and Conventions

In AR models, we have to mention the preceding nodes (${x_{<t}}$) of a specific node ($x_{t}$). For $t=5$, the relations between ${x_{<5}}$ and $x_5$ is shown in the following illustration.

There are different notations for such relations.

In Uria et al., the authors use $p(x_{o_d}\mid \mathbf x_{o_{<d}})$ [^Uria2016].
In Liu et al. and Papamakarios et al., the authors use $p(x_{t}\mid \mathbf x_{1:t-1})$ [^Liu2020][^Papamakarios2017].
In Germain et al., the authors use $p(x_t\mid \mathbf x_{<t})$ [^Germain2015].

In the current review, we expanded the vector notation $\mathbf x_{<t}$ into a set notation as it is not necessarily a vector.

Planted: 2021-08-13 by L Ma;

References: