Deep Infomax

[[Mutual information]] Mutual Information Mutual information is defined as $$ I(X;Y) = \mathbb E_{p_{XY}} \ln \frac{P_{XY}}{P_X P_Y}. $$ In the case that $X$ and $Y$ are independent variables, we have $P_{XY} = P_X P_Y$, thus $I(X;Y) = 0$. This makes sense as there would be no “mutual” information if the two variables are independent of each other. Entropy and Cross Entropy Mutual information is closely related to entropy. A simple decomposition shows that $$ I(X;Y) = H(X) - H(X\mid Y), $$ which is the reduction of … maximization is performed on the input of the encoder $X$ and the encoded feature $\hat X=E_\theta (X)$,

$$ \operatorname{arg~max}_\theta I(X;E_\theta (X)). $$

Being a quantity that is notoriously hard to compute, mutual information $I(X;E_\theta (X))$ is usually estimated using its lower bound, which depends on a choice of a functional $T_\omega$. Thus the objective will be maximizing a parametrized mutual information estimation,

$$ \operatorname{arg~max}_{\theta, \omega} \hat I_\omega(X;E_\theta (X)) $$

Local Mutual Information

To compare local features to the encoder output, we need to extract values from inside the encoder, i.e.,

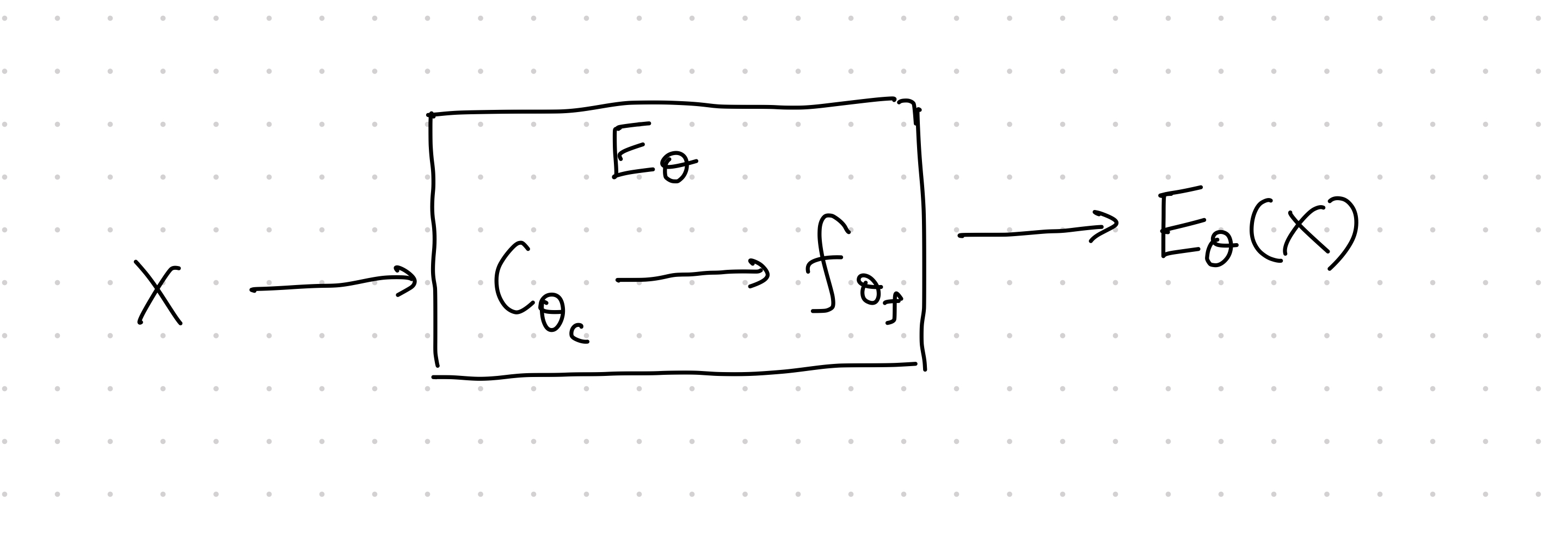
$$ E_{\theta_f, \theta_C} = f_{\theta_f} \circ C_{\theta_C}. $$

The first step, $C_{\theta_C}$ is to map the input into feature maps, the second step, $f_{\theta_f}$ maps the feature maps into the encoding. The feature map $C_{\theta_C}$ is split into patches,

$$ C_{\theta_C}= \left \{ C_\theta^{(i)} \right\}. $$

The objective is

$$ \operatorname{arg~max}_{\theta_f, \theta_C, \omega}\mathbb E_{i} \left[ \hat I_\omega( C_{\theta_C}^{(i)} ;E_\theta (X)) \right]. $$

Code

• rdevon/DIM: by the authors
• DuaneNielsen/DeepInfomaxPytorch: a clean implementation