Graph Cuts
Cut
For a subset of nodes $\mathcal A\subset \mathcal V$, the rest of nodes can be denoted as $\bar {\mathcal A} = \mathcal V \setminus \mathcal A$. In other words, $\mathcal A \cup \bar {\mathcal A} = \mathcal V$ and $\mathcal A \cap \bar {\mathcal A} = \emptyset$. That being said, the nodes can be partitioned into two subsets, $\mathcal A$ and $\bar {\mathcal A}$. The cut of this partition is defined as the total number of edges between them,
$$ \operatorname{Cut} \left( \mathcal A, \bar{\mathcal A} \right) = \frac{1}{2} \left( \lvert (u, v)\in \mathcal E: u\in \mathcal A, v\in \bar{\mathcal A} \rvert + \lvert (u, v)\in \mathcal E: u\in \bar{\mathcal A}, v\in {\mathcal A} \rvert \right). $$
To generalize this notion, suppose we partition the nodes into $k$ subsets of nodes, $\mathcal A_1, \cdots, \mathcal A_k$, the cut is the total number of edges between $\mathcal A_k$ and $\bar{\mathcal A_k}$ 1,
$$ \operatorname{Cut} \left( \mathcal A_1, \cdots, \mathcal A_k \right) = \frac{1}{2} \sum_{k=1}^K \lvert (u, v)\in \mathcal E: u\in \mathcal A_k, v\in \bar{\mathcal A_k} \rvert. $$
For smaller cut value, the proposed patches $\mathcal A_1, \cdots, \mathcal A_k$ are more disconnected from the overall graph.
This definition is biased towards smaller graphlets, i.e., smaller subset of nodes will get smaller cut values.
Ratio Cut
Ratio Cut normalizes the cut values by the size of the patches,
$$ \operatorname{RatioCut} \left( \mathcal A_1, \cdots, \mathcal A_k \right) = \frac{1}{2} \sum_{k=1}^K \frac{\lvert (u, v)\in \mathcal E: u\in \mathcal A_k, v\in \bar{\mathcal A_k} \rvert}{ \lvert \mathcal A_k \rvert}. $$
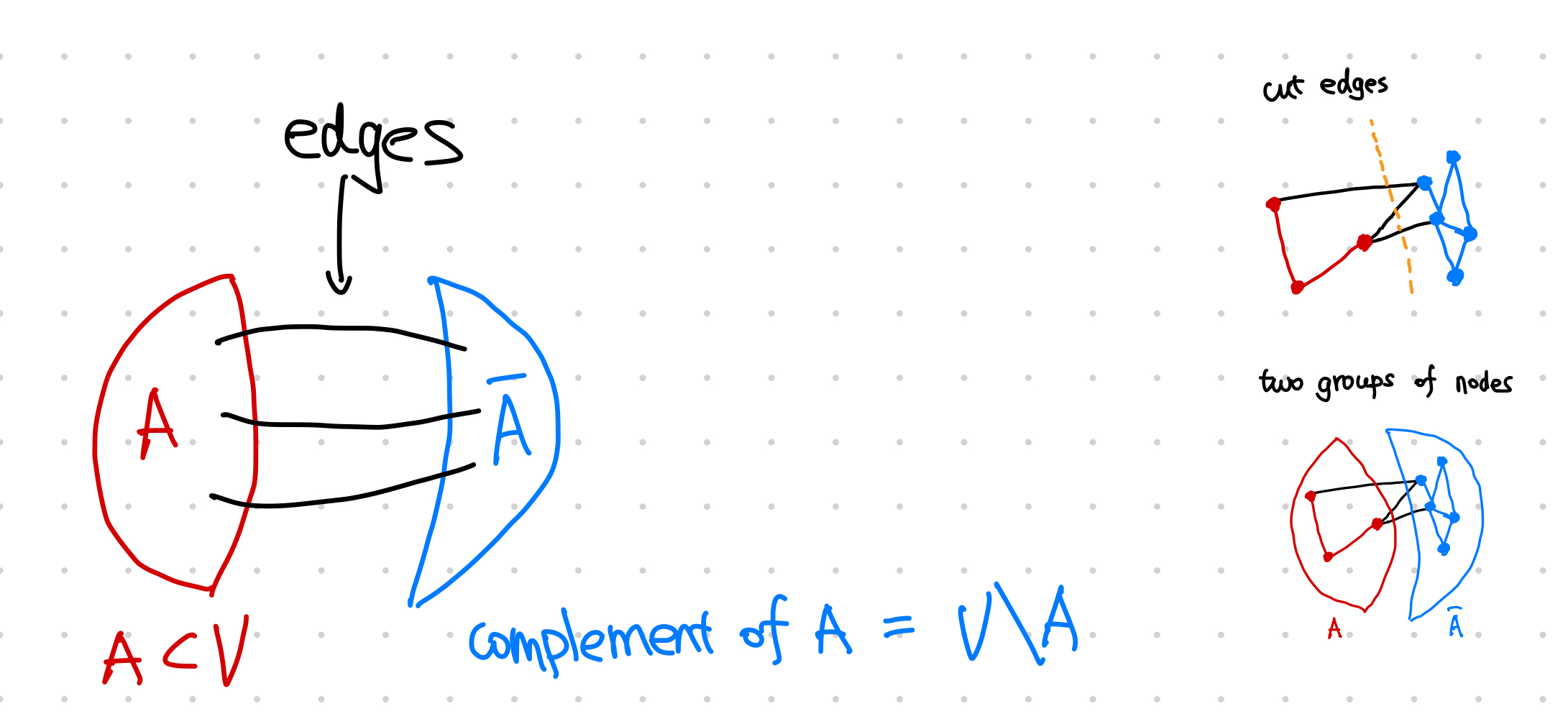
Graph cuts
This definition punishes smaller patches using $\frac{1}{ \lvert \mathcal A_k \rvert}$.
Normalized Cut
The normalized cut uses the node degrees as punishment, $\operatorname{vol}(\mathcal A_k) = \sum_{u\in\mathcal A_k} d_u$,
$$ \operatorname{NCut} \left( \mathcal A_1, \cdots, \mathcal A_k \right) = \frac{1}{2} \sum_{k=1}^K \frac{\lvert (u, v)\in \mathcal E: u\in \mathcal A_k, v\in \bar{\mathcal A_k} \rvert}{ \lvert\operatorname{vol}(A_k) \rvert}. $$
Examples
Barbell Graph
To illustrate the idea, we use a small barbell graph as an example.
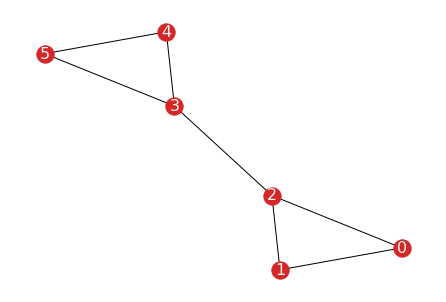
A simple barbell graph
Now we propose different partitions of the graph and calculate the cuts.
| $A_1$ | $A_2$ | Cut | RatioCut | NCut |
|---|---|---|---|---|
{0, 1, 2} | {3, 4, 5} | 1 | 0.67 | 0.29 |
{0, 1, 2, 3} | {4, 5} | 2 | 1.50 | 0.70 |
Code
import matplotlib.pyplot as plt
import networkx as nx
import numpy as np
nx_draw_style = dict(node_color="tab:red", font_size=16, font_color="whitesmoke")
def ratio_cut_size(G, S, T=None, weight=None):
if T is None:
T = set(G) - set(S)
num_cut_edges = nx.cut_size(G, S, T=T, weight=weight)
norm_S = len(S)
norm_T = len(T)
return num_cut_edges * ((1 / norm_S) + (1 / norm_T))
def compare_cuts(graph, partition):
return {
"cut": nx.cut_size(G, partition[1], partition[2]),
"ncut": nx.normalized_cut_size(G, partition[1], partition[2]),
"ratio_cut": ratio_cut_size(G, partition[1], partition[2])
}
# barbell graph
G_bb = nx.barbell_graph(3, 0)
# visualize the graph
pos = nx.spring_layout(G_bb, seed=seed)
nx.draw(G_bb, pos=pos, with_labels = True, **nx_draw_style)
plt.show()
# two different partitions
partition_bb_1 = {
1: {0, 1, 2},
2: {3, 4, 5}
}
partition_bb_2 = {
1: {0, 1, 2, 3},
2: {4, 5}
}
# calculate the cuts for the two different partitions
compare_cuts(
G_bb, partition_bb_1
), compare_cuts(
G_bb, partition_bb_2
)
cards/graph/graph-cuts:L Ma (2021). 'Graph Cuts', Datumorphism, 09 April. Available at: https://datumorphism.leima.is/cards/graph/graph-cuts/.