State Space Models
State space model is an important category of model for sequential data. Through simple assumptions, state space models can achieve quite complicated distributions.
To model a sequence, we can use the joint probability of all the nodes,
$$ p(x_1, x_2, \cdots, x_N), $$
where $x_i$ are the nodes in the sequence.
Orders
We can introduce different order of dependencies on the past.
The simplest model for the sequence is assuming i.i.d..

Each node is independent of each other
To model the dependencies in the sequence, we can assume a node depends on the previous nodes. The first-order model assume that node $x_{i+1}$ only depends on node $x_i$.
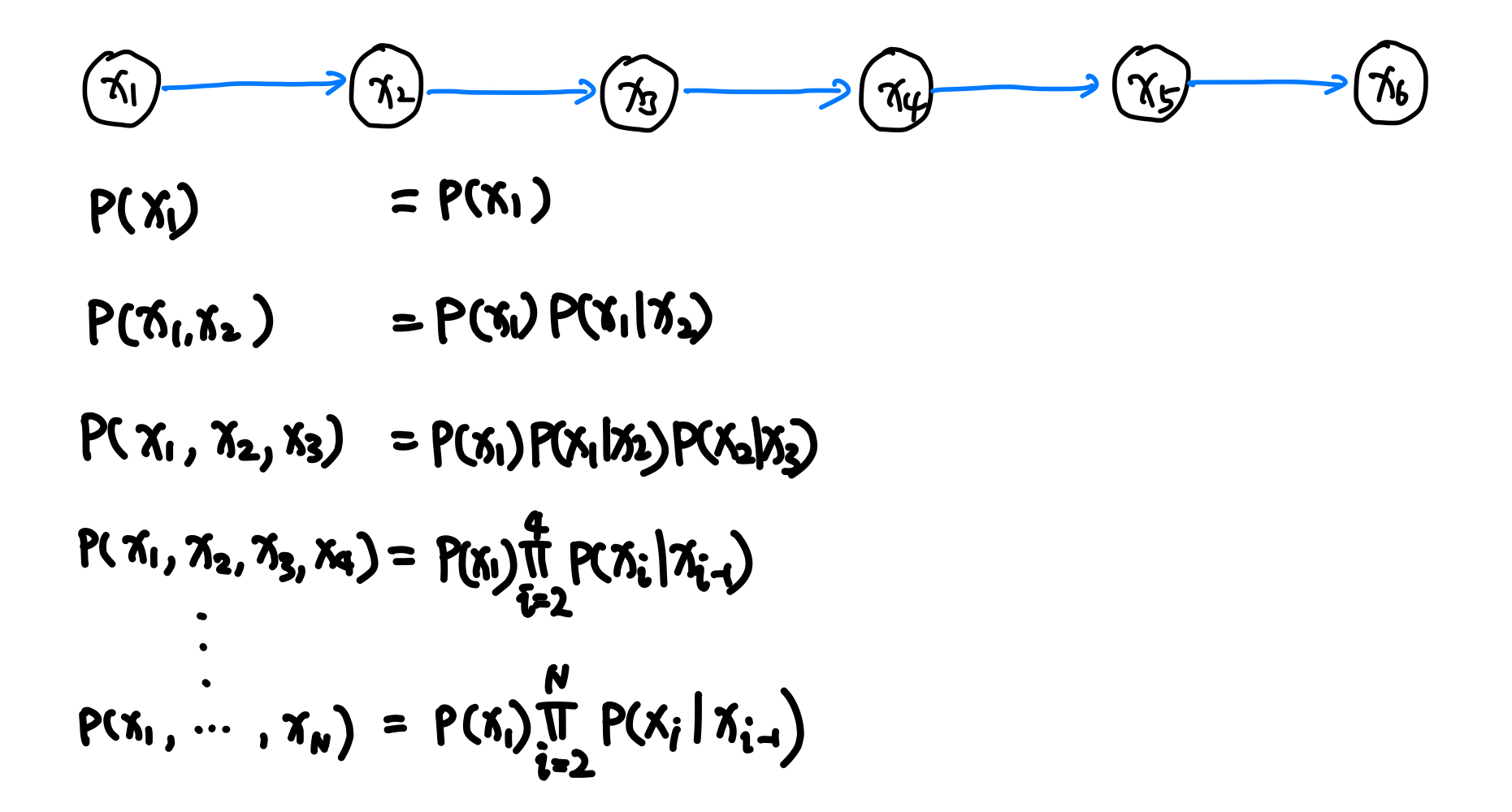
Each node depends on the previous node
To add more complexities, we introduce the second order model.

Each node depends on the previous two nodes
Hidden States
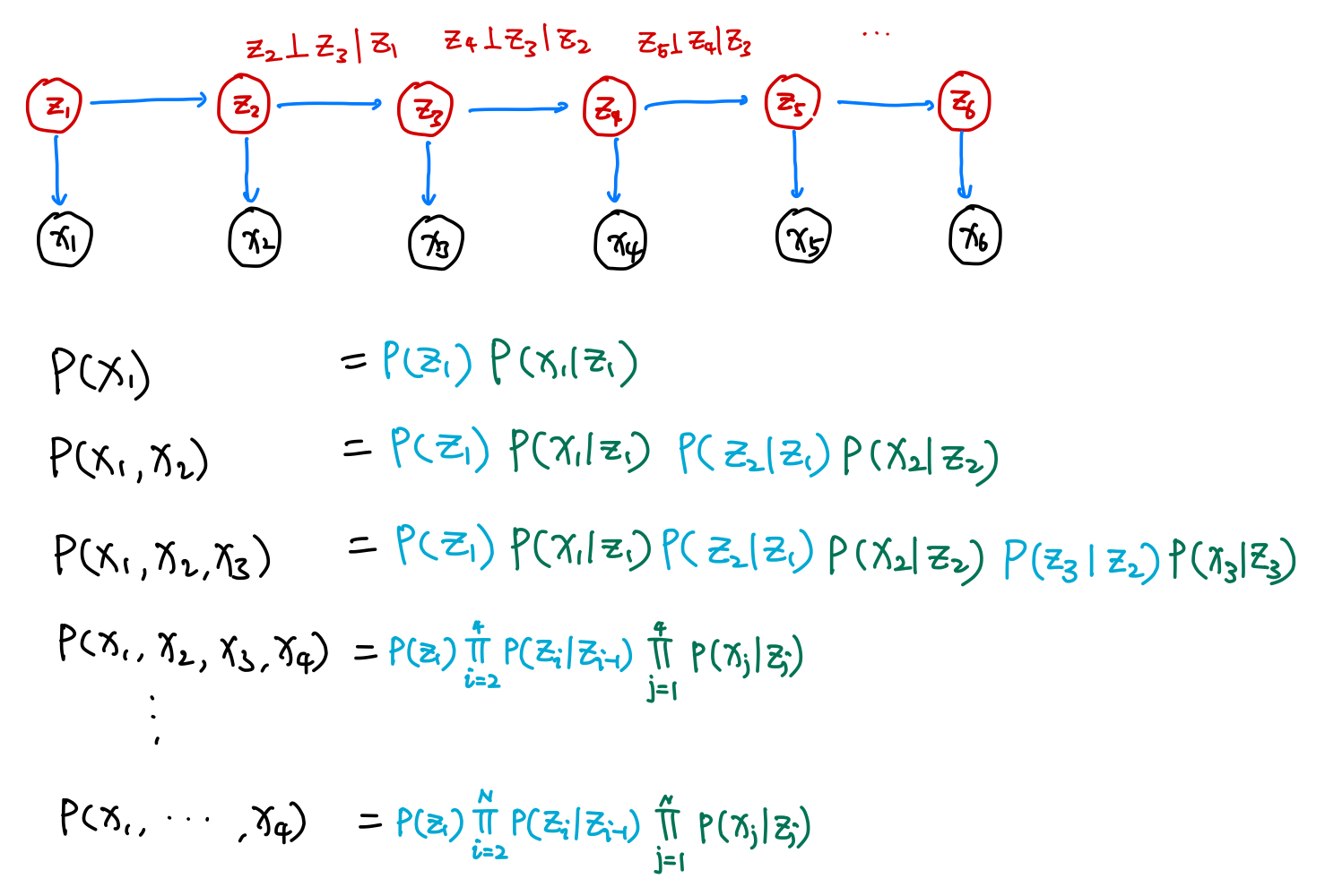
For some quantities, such as the GMV of a company, we expect that the dynamics of them are driven by some other factors, which data we may not have.
We introduce a latent space $\{z_i\}$ which is described by first order process. The visible states $\{x_i\}$ are determined using $p(x_i\vert z_i)$ 1.
wiki/time-series/state-space-models:wiki/time-series/state-space-models Links to:LM (2022). 'State Space Models', Datumorphism, 02 April. Available at: https://datumorphism.leima.is/wiki/time-series/state-space-models/.