Statistical Hypothesis Testing
When we have a sample of the population, we immediately calculate the mean using the sample, say the result is $\mu_0$. Of course, the population mean $\mu_p$ is unknown and probably can never be known.
This specific sample mean $\mu_0$ is nothing but like an advanced educated guess. Then again, how do we know if our this specific sample mean $\mu_0$ is a faithful representation of the population mean? In fact, this question is not limited to mean. It applies to any statistical measurement.
The hypothesis testing theory solution to this problem is to tell whether our hypothesis is correct.
To explain this method, we have to establish two hypotheses for our statistical result. We will still use the mean as the measurement. For example, we could have the two hypotheses:
- Null hypothesis $H_0$: the population mean $\mu_p$ equals to this specific educated guess $\mu_0$.
- Alternative hypothesis $H_a$: the population mean $\mu_p$ doesn’t equal to our educated guess $\mu_0$.
The hypotheses themselves could be much more general but we always have a null hypothesis and alternative hypothesis.
Hypothesis testing is in fact related to conditional probability. To see this, we reformulate our statistical procedures.
- We get an educated guess of our population mean, $\mu_p = \mu_0$.
- We set up the null hypothesis and alternative hypothesis.
- $H_0$: the population mean $\mu_p$ equals to this specific educated guess $\mu_0$.
- $H_a$: the population mean $\mu_p$ doesn’t equal to our educated guess $\mu_0$.
- We draw samples from our population and calculate the sample mean $\mu_i$, where $i$ is used to label the samples.
- Then we ask the question: Are the sample means tolerable assuming the null hypothesis is true? In other words, we are calculating $$ P( \text{sample mean is located at } \mu_i | \text{null hypothesis is true} ) $$
However, the conclusion from hypothesis testing is only about whether the null hypothesis is accepted or rejected, nothing more. In our example:
- We can NOT determine what mean value to take if the hypothesis is rejected.
- We can NOT understand how likely our educated guess $\mu_p = \mu0$ is true. The probability we calculated is about the sample not the hypothesis.
As mentioned, it doesn’t have to be related to the mean value. We can do hypothesis test on other statistical measurements. The above example also hints that there can be [[different types of mistakes]] Types of Errors in Statistical Hypothesis Testing We all make mistakes. The question is, what kind of mistakes. from a hypothesis test.
Choosing a test method
A map on this topic: Map
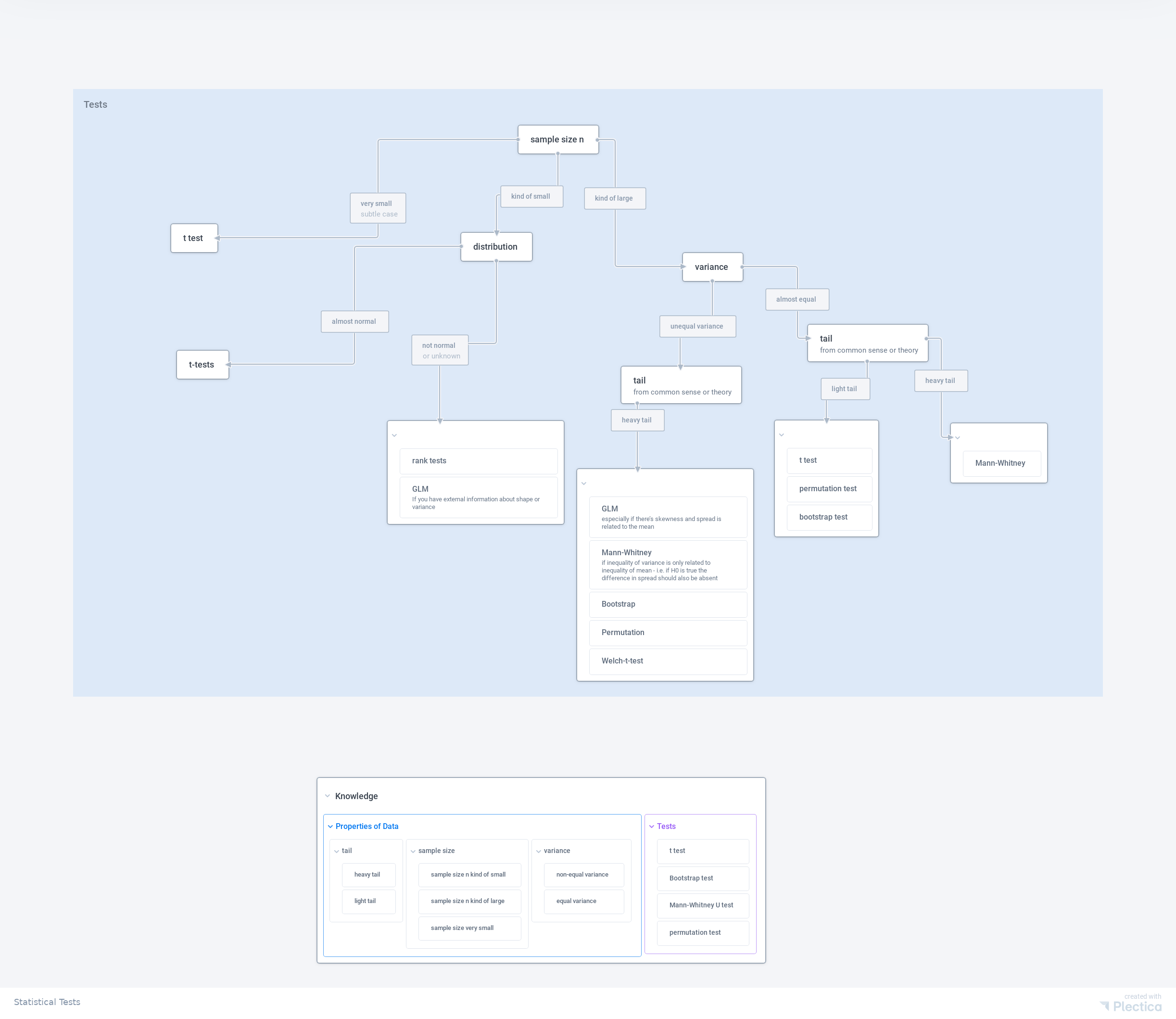
A map of hypothesis testing. Made on Plectica.
wiki/statistical-hypothesis-testing/hypothesis-testing:wiki/statistical-hypothesis-testing/hypothesis-testing Links to:L Ma (2019). 'Statistical Hypothesis Testing', Datumorphism, 01 April. Available at: https://datumorphism.leima.is/wiki/statistical-hypothesis-testing/hypothesis-testing/.