Receiver Operating Characteristics: ROC
ROC space is the two-dimensional space spanned by True Positive Rate and False Positive Rate.
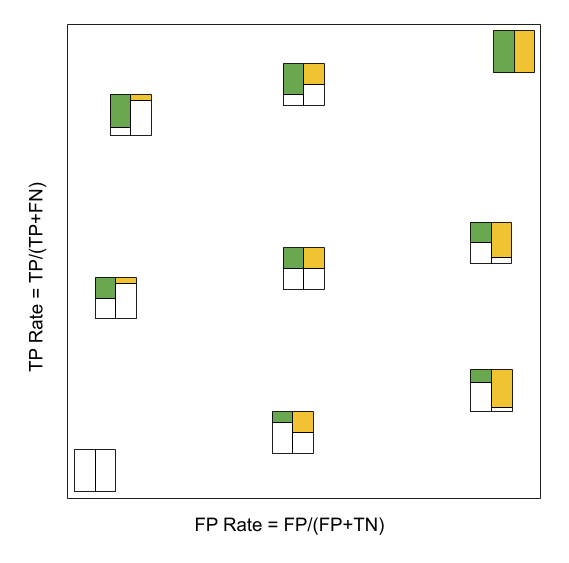
ROC Space. The color boxes are indicating the confusion matrices. Green is the fraction of true positive. Orange is the fraction of false positive. Refer to Confusion Matrix for more details.
AUC: Area under Curve
- TPR = TP Rate
- FPR = FP Rate
The ROC curve is defined by the relation $f(TPR, FPR)$. Area under the ROC curve is
$$ \int TPR(FPR) d(FPR) \sim \sum_i TPR_i *\Delta FPR. $$
If AUC = 1, we have TP Rate = 1 for all FP Rate. This is the best performance a model could have.
How to Calculate ROC Curve
Not every model has an AUC. To get the AUC curve, we need a hyperparameter to be tuned to get different TP Rate and FP Rate.
In logistic regression, a threshold $T$ is predetermined to decide which label to use in classifications.
By tuning the threshold $T$, we get different TP Rate $TPR$ and FP Rate $FPR$, i.e., $TPR(T)$ and $FPR(T)$. The parametric relations between $TPR(T)$ and $FPR(T)$ forms the ROC curve.
wiki/machine-learning/performance/roc:wiki/machine-learning/performance/roc Links to:L Ma (2020). 'Receiver Operating Characteristics: ROC', Datumorphism, 05 April. Available at: https://datumorphism.leima.is/wiki/machine-learning/performance/roc/.