Machine Learning Overview

#Statistical Learning #Machine Learning #Basics

What is Machine Learning

Abu-Mostafa, Magdon-Ismail, and Lin summarized machine learning problem using the following chart ¹ ². Ultimately, we need to find an approximation $g$ of the true map $f$ from features $\mathcal X$ to targets $\mathcal Y$ on a specific probability distribution of features $P$. This process is done by using an algorithm to select some hypothesis that works.

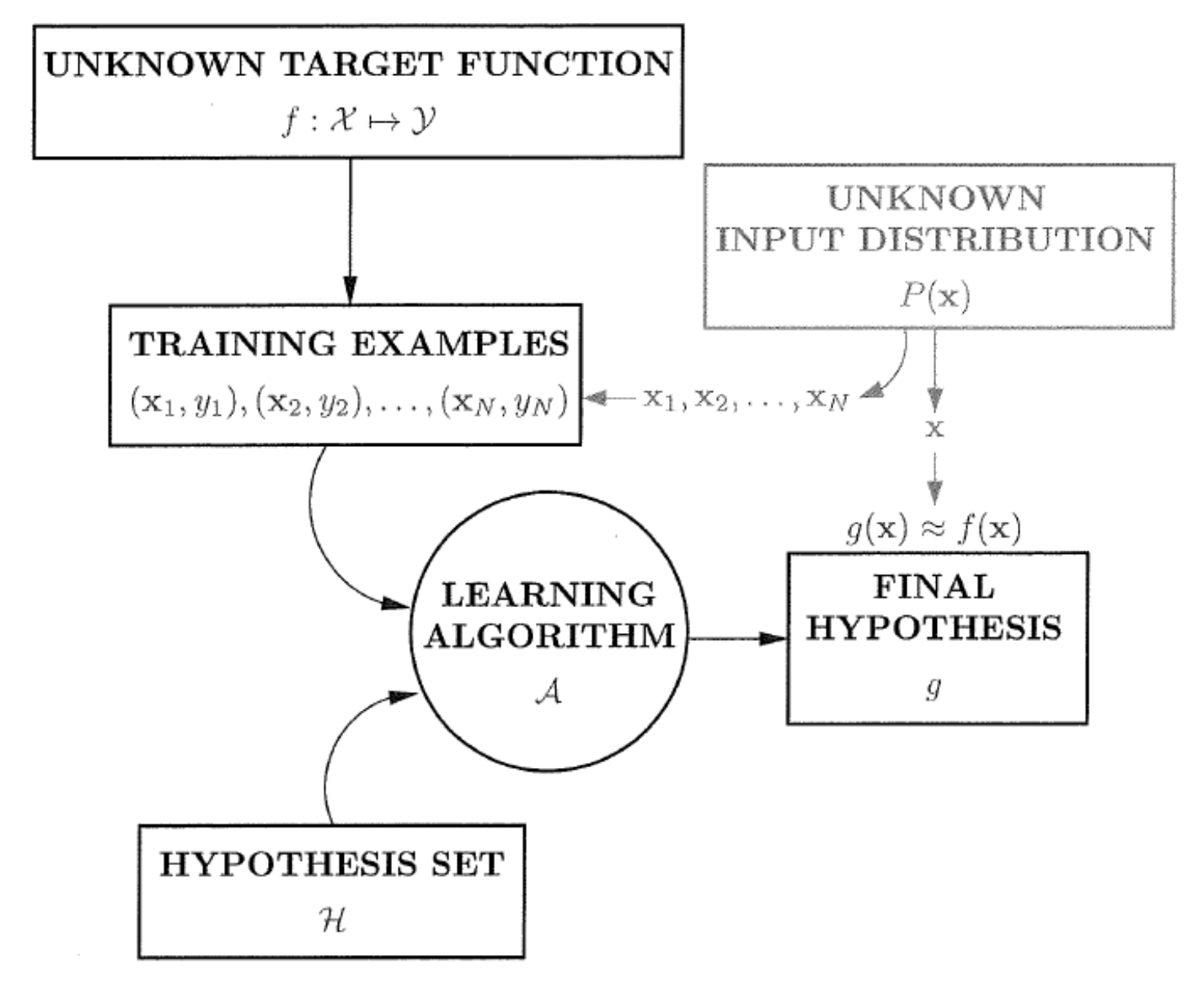
From the book Learning From Data by Abu-Mostafa, Magdon-Ismail, and Lin. I am using a version by Deckert. — From the book *Learning From Data* by Abu-Mostafa, Magdon-Ismail, and Lin. I am using a version by Deckert.

In the core of machine learning models, we have three components³:

Representation: encode data and problem representation, i.e., propose a space to set a stage.
Evaluation: an objective function to be evaluated that guides the model.
Optimization: an algorithm to optimize the model so it learns what we want it to do.

Machine Learning Workflow

There are many objectives in machine learning. Two of the most applied objectives are classifications and regressions. In classifications and regression, the following four factors are relevant.

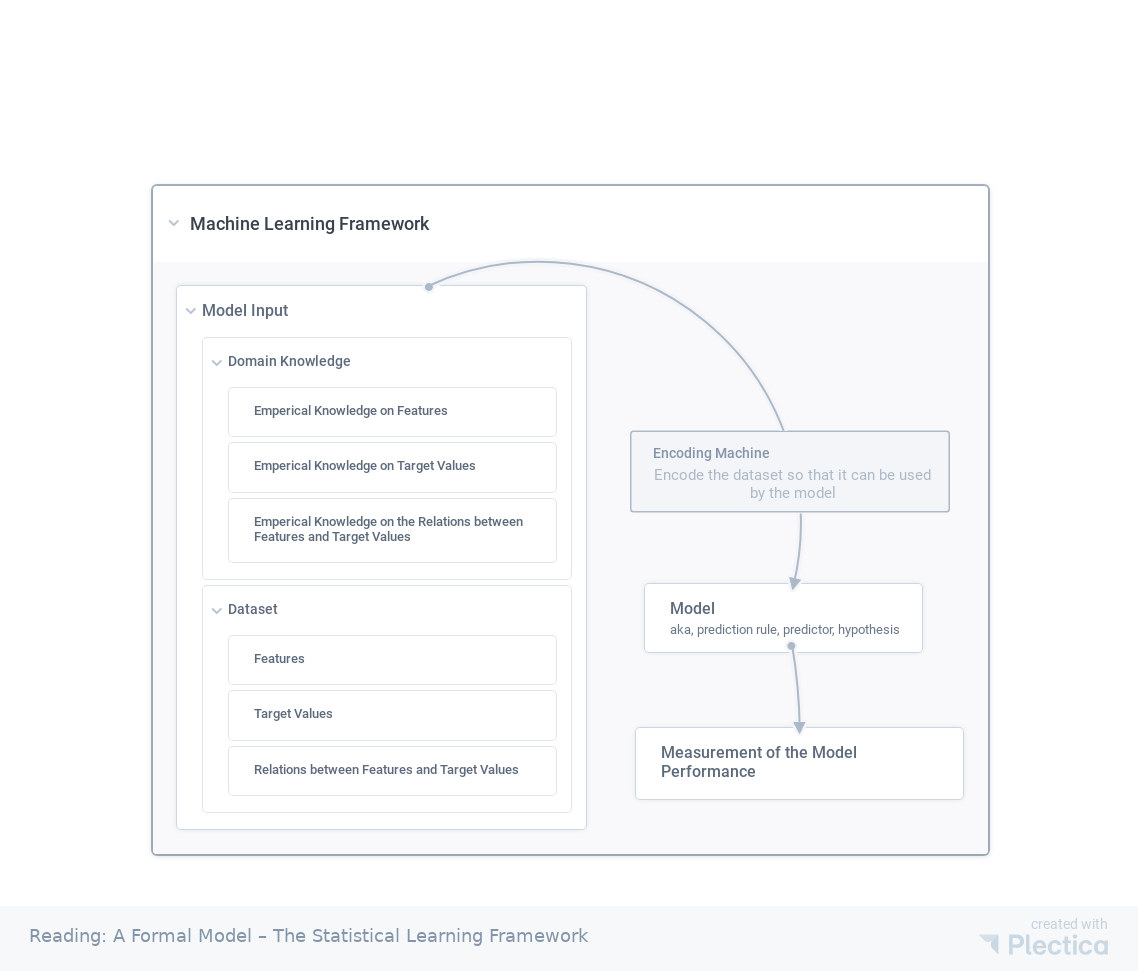
A simple framework of machine learning. The dataset $\tilde{\mathscr D}$ is first encoded by $\mathscr T$, $\mathscr D(\mathbf X, \mathbf Y) = \mathscr T(\tilde{\mathscr D})$. The dataset is feeded into the model, $\bar{\mathbf Y} = f(\mathbf X;\mathbf \theta)$. The model is then tested with the test method, $L_{f, \mathscr D}(h)$. By requiring the test method to satisfy some specific conditions, we solve the model parameters $\mathbf\theta$.

Input:
1. Domain knowledge $\tilde{\mathscr K_D}$.
  1. on features,
  2. on target values,
  3. on relation between features and target values.
2. A dataset $\tilde{\mathscr D}(\tilde{\mathbf X}, \tilde{\mathbf Y})$ with $\tilde{\mathbf X}$ being the features and $\tilde{\mathbf Y}$ being the values to be predicted;
  1. features (domain set): $\tilde{\mathbf X}$,
  2. target values (label set): $\tilde{\mathbf Y}$.
  3. relations between features and target values: $f(\mathbf X) \to \mathbf Y$.
A set of “encoders” $\mathscr T_i$ that maps the features $\tilde{\mathbf X}$ into machine-readable new features $\mathbf X$ and predicting values $\tilde{\mathbf y}$ into machine readable new values $\mathbf y$. The dimensions of $\tilde{\mathbf X}$ and $\mathbf X$ may not be the same. In summary, $\mathscr T(\tilde{\mathscr D}) \to \mathscr D$.
A model (aka, prediction rule, predictor, hypothesis) $h(\mathbf X;\mathbf \theta)\to \bar{\mathbf Y}$ that maps $\mathbf X$ to the values with $\mathbf X$ being a set of input features. $h$ may also be a set of functions.
A measurement of the model performance, $L_{f, \mathscr D}(h)$.
1. Error of model: $L_{f, \mathscr D}(h) = \mathscr L(h(\mathbf X), f(\mathbf X))$, where $\mathscr L$ is distance operator.