Logistic Regression
In a classification problem, given a list of features values $x$ and their corresponding classes $\{c_i\}$, the posterior for of the classes, aka conditional probability of the classes, is
$$ p(C=c_i\mid X=x). $$
Logistic Regression for Two Classes
For two classes, the simplest model for the posterior is a linear model,
$$ \log \frac{p(C=c_1\mid X=x) }{p(C=c_2\mid X=x)} = \beta_0 + \beta_1 \cdot x, $$
which is equivalent to
$$ p(C=c_1\mid X=x) = \exp\left(\beta_0 + \beta_1 \cdot x\right) p(C=c_2\mid X=x) . $$
Using the normalization condition
$$ p(C=c_1\mid X=x) + p(C=c_2\mid X=x) = 1, $$
we can derive the posterior for each classes
$$ \begin{align} p(C=c_2\mid X=x) &= \frac{1}{1 + \exp\left(\beta_0 + \beta_1 \cdot x\right)} \\ p(C=c_1\mid X=x) &= \frac{\exp\left(\beta_0 + \beta_1 \cdot x\right)}{1 + \exp\left(\beta_0 + \beta_1 \cdot x\right)}. \end{align} $$
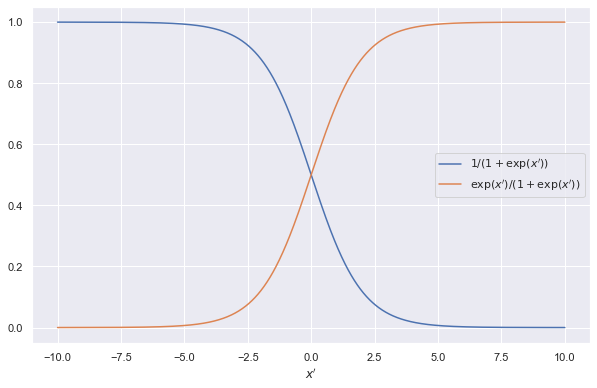
For simplicity, we are using $x’=\beta_0 + \beta_1 \cdot x$ in this figure.
This is the [[sigmoid function]] Uni-Polar Sigmoid Uni-polar sigmoid function and its properties
Relation to Cross Entropy
For two classes, we can write down the likelihood as
$$ \pi_{i=1}^{N} p^{y_i} p^{1-y_i}, $$
where $p$ is the probability of label $y_i=c_1$ and $1-p$ is probability of label $y_i=c_2$.
Taking the neglog, we find that
$$ -l = sum_{i=1}^N ( -y_i \log p - (1-y_i)\log (1-p) ). $$
This is the [[cross entropy]] Cross Entropy Cross entropy is1 $$ H(p, q) = \mathbb E_{p} \left[ -\log q \right]. $$ Cross entropy $H(p, q)$ can also be decomposed, $$ H(p, q) = H(p) + \operatorname{D}_{\mathrm{KL}} \left( p \parallel q \right), $$ where $H(p)$ is the [[entropy of $P$]] Shannon Entropy Shannon entropy $S$ is the expectation of information content $I(X)=-\log \left(p\right)$1, \begin{equation} H(p) = \mathbb E_{p}\left[ -\log \left(p\right) \right]. \end{equation} shannon_entropy_wiki Contributors to Wikimedia projects. …
Logistic Regression for $K$ Classes
It is easily generalized to problems with $K$ classes.
$$ \begin{align} p(C=c_K\mid X=x) &= \frac{1}{1 + \sum_k\exp\left(\beta_{k0} + \beta_k \cdot x\right)} \\ p(C=c_k\mid X=x) &= \frac{\exp\left(\beta_{k0} + \beta_k \cdot x\right)}{1 + \sum_k\exp\left(\beta_{k0} + \beta_k \cdot x\right)} \end{align} $$
Why not non-linear
The log of the posterior ratio can be more complex than linear models. In general, we have1
$$ \log \frac{p(C=c_1\mid X=x) }{p(C=c_2\mid X=x)} = f(x), $$
so that
$$ p(C=c_1\mid X=x) = \frac{\exp(f(x))}{ 1 + \exp(f(x)) }. $$
The logistic regression model we mentioned in the previous sections require
$$ f(x) = \beta_0 + \beta_1 \cdot x. $$
A more general additive model is
$$ f(x) = \sum_i f_i(x), $$
where we can apply algorithms such as local scoring to fit such models1.
- Hastie T, Tibshirani R, Friedman J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction. Springer Science & Business Media; 2013. pp. 567–567. Available: https://play.google.com/store/books/details?id=yPfZBwAAQBAJ
- friedman2000 Friedman J, Hastie T, Tibshirani R. Additive Logistic Regression. The Annals of Statistics. 2000. pp. 337–374. doi:10.1214/aos/1016218223
- Mehta2019 Mehta P, Wang C-H, Day AGR, Richardson C, Bukov M, Fisher CK, et al. A high-bias, low-variance introduction to Machine Learning for physicists. Phys Rep. 2019;810: 1–124. doi:10.1016/j.physrep.2019.03.001
wiki/machine-learning/linear/logistic-regression:wiki/machine-learning/linear/logistic-regression Links to:L Ma (2021). 'Logistic Regression', Datumorphism, 05 April. Available at: https://datumorphism.leima.is/wiki/machine-learning/linear/logistic-regression/.