Contrastive Predictive Coding
Contrastive Predictive Coding, aka CPC, is an autoregressive model combined with InfoNCE loss1.
There are two key ideas in CPC:
- Autoregressive models in latent space, and
- InfoNCE loss that combines mutual information and [[NCE]] Noise Contrastive Estimation: NCE Noise contrastive estimation (NCE) objective function is1 $$ \mathcal L = \mathbb E_{x, x^{+}, x^{-}} \left[ - \ln \frac{ C(x, x^{+})}{ C(x,x^{+}) + C(x,x^{-}) } \right], $$ where $x^{+}$ represents data similar to $x$, $x^{-}$ represents data dissimilar to $x$, $C(\cdot, \cdot)$ is a function to compute the similarities. For example, we can use $$ C(x, x^{+}) = e^{ f(x)^T f(x^{+}) }, $$ so that the objective function becomes $$ \mathcal L = \mathbb E_{x, x^{+}, x^{-}} \left[ - \ln \frac{ e^{ … .
For the series of segments, ${x_t}$, we apply an encoder on each segment, and calculate the latent space, ${{\color{blue}\hat x_t}}$. The latent space ${{\color{blue}\hat x_t}}$ is then modeled using an autoregressive model to calculate the coding, ${{\color{red}c_t}}$.
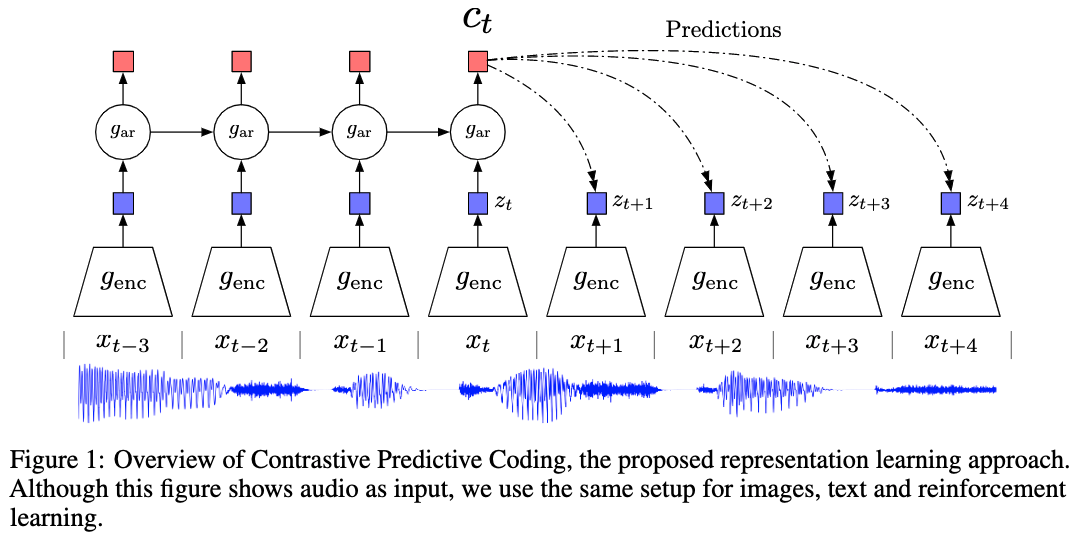
van den Oord et al
The loss is built on NCE to estimate the lower bound of mutual information,
$$ \mathcal L = -\mathbb E_X \left[ \log \frac{f_k(x_{t+k}, c_t)}{\sum_{j} f_k(x_{j}, c_t) } \right], $$
where $f_k(x_{x+i}, c_t)$ is estimated using a log-bilinear model, $f_k(x_{x+i}, c_t) = \exp\left( z_{t+i} W_i c_t \right)$. This is also a cross entropy loss.
Minimizing $\mathcal L$ leads to a $f_k$ that estimates the ratio1
$$ \frac{p(x_{t+k}\mid c_t)}{p(x_{t+k})} = \frac{p(x_{t+k}, c_t)}{p(x_{t+k})p(c_t)}. $$
We can perform downstream tasks such as classifications using the encoders.
Code
wiki/machine-learning/contrastive-models/contrastive-predictive-codeing Links to:L Ma (2021). 'Contrastive Predictive Coding', Datumorphism, 09 April. Available at: https://datumorphism.leima.is/wiki/machine-learning/contrastive-models/contrastive-predictive-codeing/.