What is Graph
Graph
A graph $\mathcal G$ has nodes $\mathcal V$ and edges $\mathcal E$,
$$ \mathcal G = ( \mathcal V, \mathcal E). $$

Representations of Graph
There are different representations of a graph.
Adjacency Matrix
A adjacency matrix of a graph represents the nodes using row and column indices and edges using elements of the matrix.
For simple graph, the adjacency matrix is rank two and dimension $\lvert \mathcal V \rvert \times \lvert \mathcal V \rvert$. For edge $(u, v)\in \mathcal E$, it is represented by the matrix element $\mathbf A[u,v]=1$.
See Sanchez-Lengeling, 2021 for an interactive example1.
Laplacians
Laplacians are transformations of the adjacency matrix but provides a lot more convenience for analysis.
Laplacian is a useful representation of graphs. The unnormalized Laplacian is
\mathbf L = \mathbf D - \mathbf A,
where $\mathbf A$ is the and $\mathbf D$ is the degree matrix, i.e., a diagonalized matrix with the diagonal elements being the degrees.
Normalized Laplacian
The symmetric normalized Laplacian is
\mathbf L_{\text{sym}} = \mathbf D^{-1/2} \mathbf A \mathbf D^{-1/2}.
The eigenvalues of normalized Laplacian is bounded ($$).
The random walk Laplacian is
\mathbf L_{\text{RW}} = \mathbf …
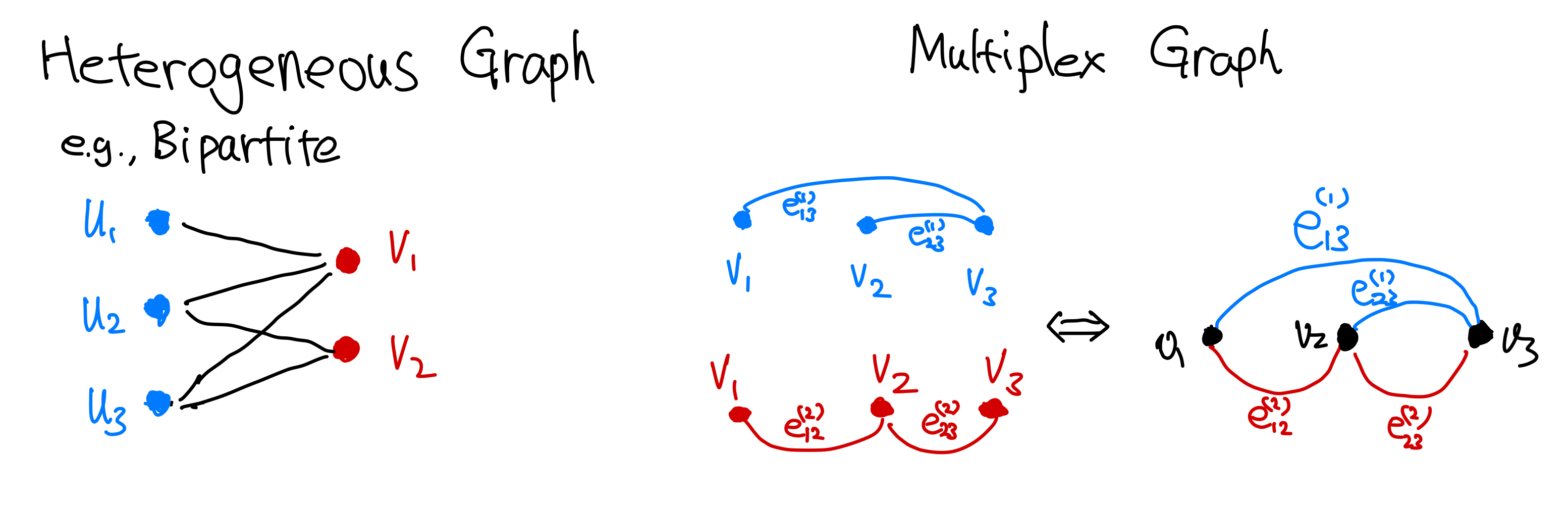
Multi-Relational Graph
A graph may have different types of edges, $\tau\in \mathcal R$, where $R$ is a set of types of relations. A multi-relational graph is then
$$ \begin{align} u &\in \mathcal V \\ v &\in \mathcal V \\ \tau &\in \mathcal R \\ (u, \tau, v) &\in \mathcal E. \end{align} $$
Two popular examples:
- heterogeneous
- multipartite
- multiplex
Heterogeneous
Nodes are subsets without intersections, $\mathcal V = \mathcal V_1\cup \mathcal V_2 \cdots \mathcal V_k$ and $\mathcal V_i \cap \mathcal V_j = \emptyset$ for $\forall i\neq j$.
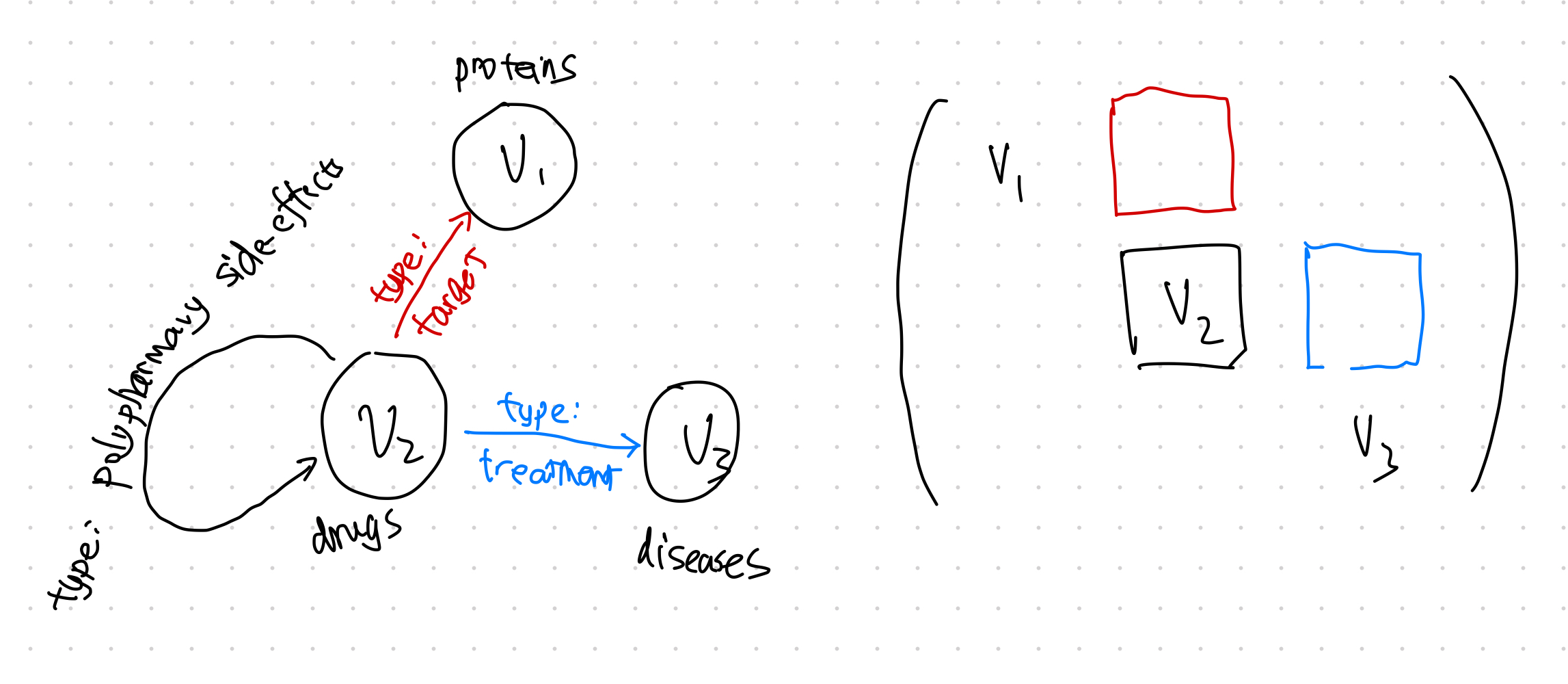
Heterogeneous graph example. A visualization of the example in Hamilton2020.
The famous multi-partite graph is an example of heterogeneous graph.
Mutiplex
The nodes can be viewed to exist in different layers and the edges in each layer are different.
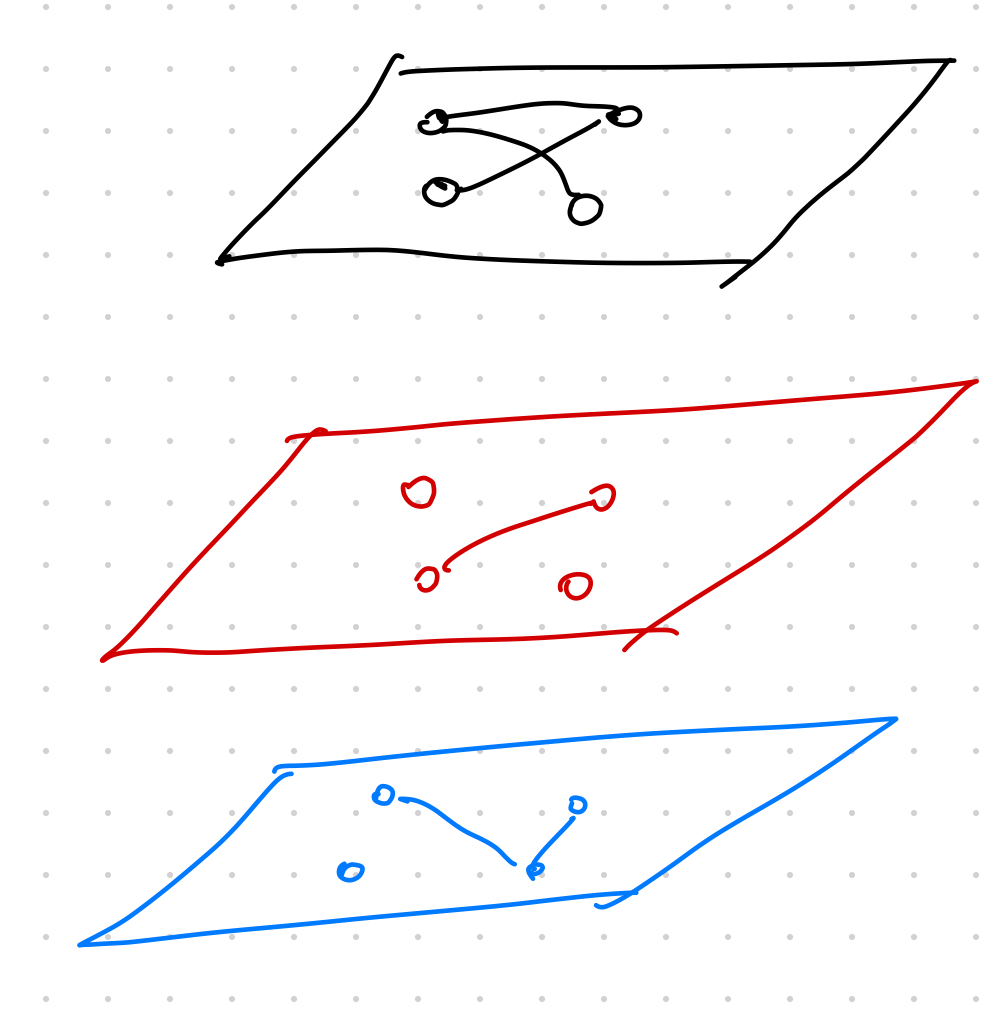
Multiplex graph example.
- Hamilton2020 Hamilton WL. Graph Representation Learning. Morgan & Claypool Publishers; 2020. pp. 1–159. doi:10.2200/S01045ED1V01Y202009AIM046
- Sanchez-Lengeling2021 Sanchez-Lengeling B, Reif E, Pearce A, Wiltschko AB. A Gentle Introduction to Graph Neural Networks. Distill. 2021;6. doi:10.23915/distill.00033
wiki/graph/basics/what-is-graph:wiki/graph/basics/what-is-graph Links to:L Ma (2021). 'What is Graph', Datumorphism, 09 April. Available at: https://datumorphism.leima.is/wiki/graph/basics/what-is-graph/.