The Time Series Forecasting Problem

There are many different types of tasks on time series data:

• classification,
• anomaly detection,
• forecasting.

Forecasting Problem

A time series forecasting problem can be formulated as the following.

Given a dataset $\mathcal D$, with

1. $y^{(i)}_t$, the sequential variable to be forecasted,
2. $x^{(i)}_t$, exogenous data for the time series data,
3. $u^{(i)}_t$, some features that can be obtained or planned in advance,

where ${}^{(i)}$ indicates the $i$th variable, ${}_ t$ denotes time. In a forecasting task, we use $y^{(i)} _ {t-K:t}$, $x^{(i) _ {t-K:t}}$, and $u^{(i)} _ {t-K:t+H}$, to forecast the future $y^{(i)} _ {t+1:t+H}$.

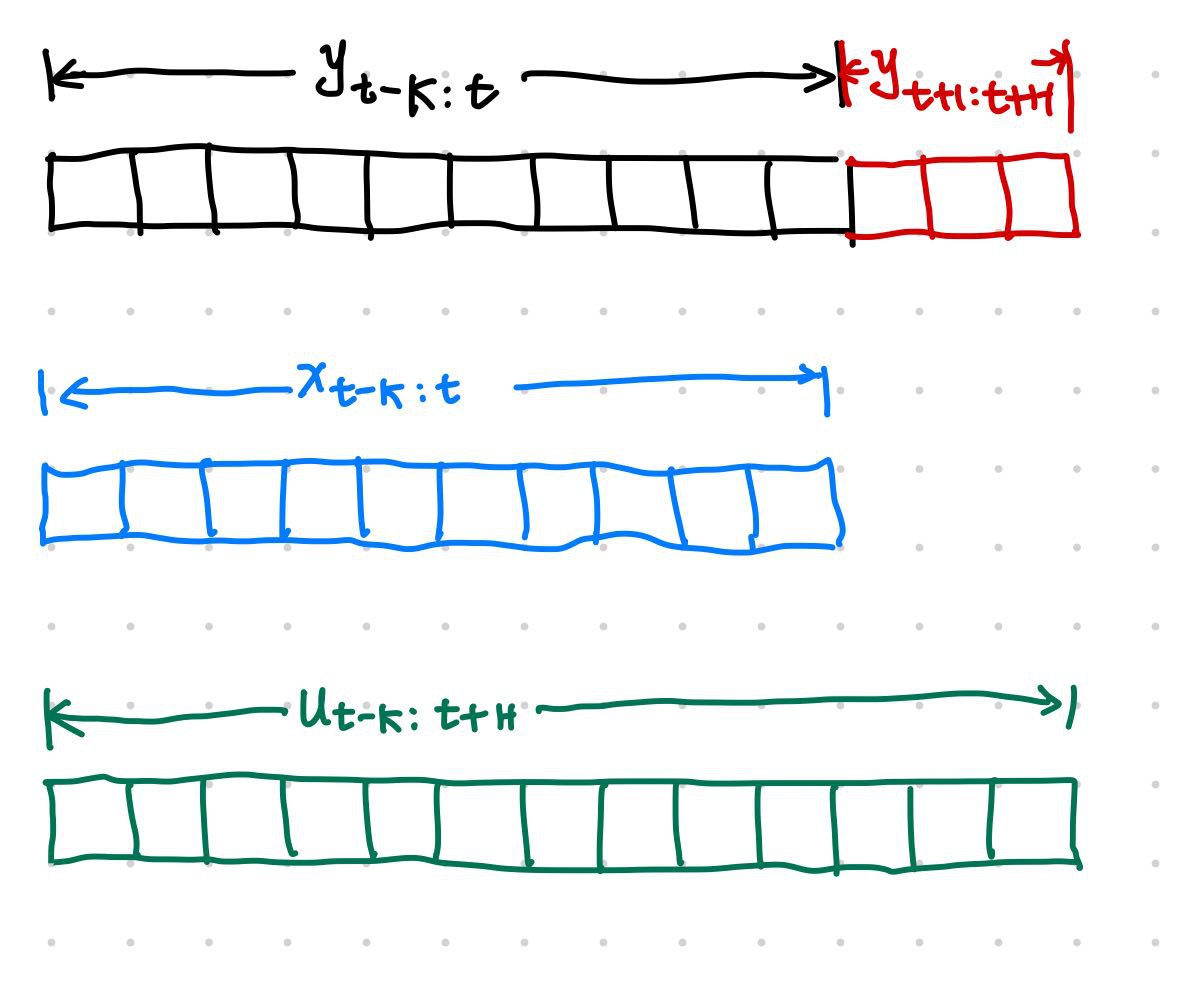
A model $f$ will use $x^{(i)} _ {t-K:t}$ and $u^{(i)} _ {t-K:t+H}$ to forecast $y^{(i)} _ {t+1:t+H}$.

The above formulation is mostly focusing on the point forecasts. Alternative, the [[probabilistic view]] Prediction Space in Forecasting In a forecasting problem, we have $\mathcal P$, the priors, e.g., price and demand is negatively correlated, $\mathcal D$, available dataset, $Y$, the observations, and $F$, the forecasts. Information Set $\mathcal A$ The priors $\mathcal D$ and the available data $\mathcal P$ can be summarized together as the information set $\mathcal A$. Under a probabilistic view, a forecaster will find out or approximate a CDF $\mathcal F$ such that1 $$ \mathcal F(Y\vert \mathcal D, \mathcal P) \to F. $$ … of a forecasting problem has been a very hot topic in recent years.

The Time Delay Embedding Representation

The time delay embedding representation of a time series forecasting problem is a concise representation of the forecasting problem ¹.

For simplicity, we only write down the representation for a problem with time series $y_{1}, \cdots, y_{t}$, and forecasting $y_{t+1}$. We rewrite the series into a matrix, in an autoregressive way,

$$ \begin{align} \mathbf Y = \begin{bmatrix} y_1 & y_2 & \cdots & y_p &\Big| & {\color{red}y_{p+1}} \\ y_{1+1} & y_{1+2} & \cdots & y_{1+p} &\Big| & {\color{red}y_{1+p+1}} \\ \vdots & \vdots & \ddots & \vdots &\Big| & {\color{red}\vdots} \\ y_{i-p+1} & y_{i-p+2} & \cdots & y_{i} &\Big| & {\color{red}y_{i+1}} \\ \vdots & \vdots & \ddots & \vdots &\Big| & {\color{red}\vdots} \\ y_{t-p+1} & y_{t-p+2} & \cdots & y_{t} &\Big| & {\color{red}y_{t+1}} \\ \end{bmatrix} \end{align} $$

which indicates that we will use everything on the left, a matrix of shape $(t-p+1,p)$, to predict the vector on the right (in red).

Methods of Forecasting Methods

T. Januschowsk et al proposed a framework to classify the different forecasting methods.²