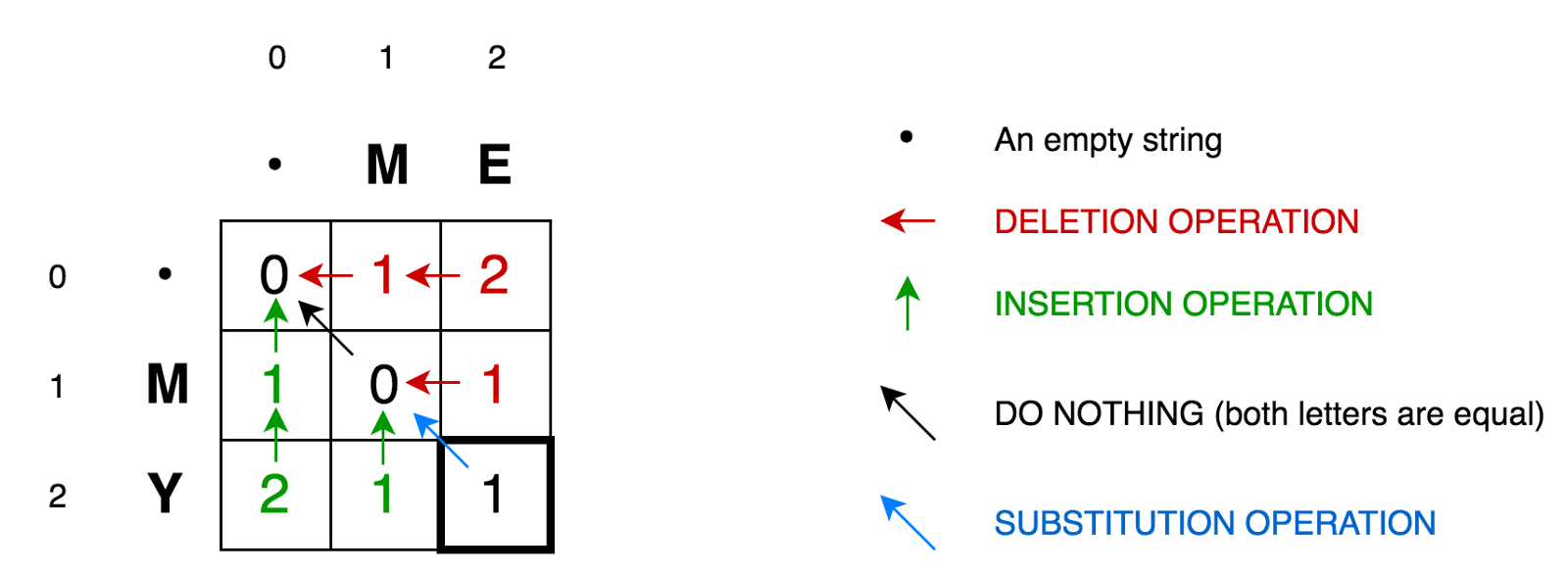
Levenshtein Distance

#Distance #NLP

Levenshtein distance calculates the number of operations needed to change one word to another by applying single-character edits (insertions, deletions or substitutions).

The reference explains this concept very well. For consistency, I extracted a paragraph from it which explains the operations in Levenshtein algorithm. The source of the following paragraph is the first reference of this article.

Levenshtein Matrix

Cell (0:1) contains red number 1. It means that we need 1 operation to transform M to an empty string. And it is by deleting M. This is why this number is red.
Cell (0:2) contains red number 2. It means that we need 2 operations to transform ME to an empty string. And it is by deleting E and M.
Cell (1:0) contains green number 1. It means that we need 1 operation to transform an empty string to M. And it is by inserting M. This is why this number is green.
Cell (2:0) contains green number 2. It means that we need 2 operations to transform an empty string to MY. And it is by inserting Y and M.
Cell (1:1) contains number 0. It means that it costs nothing to transform M into M.
Cell (1:2) contains red number 1. It means that we need 1 operation to transform ME to M. And it is by deleting E.
And so on…

From: levenshtein-distance @ trekhleb/javascript-algorithms

Examples

Word One

Characters: (( sentenceOneWords ))

Word Two

Characters: (( sentenceTwoWords ))

Levenshtein Distance: (( levenshteinDistance ))

Planted: 2019-05-19 by L Ma;

References:

levenshtein-distance @ trekhleb/javascript-algorithms