Hyperbolic Tanh

GROWING This note is being developed. It is readible but changes are being applied.
cards/machine-learning/neural-networks/activation-hyperbolic-tangent.md Current Note ID: The unique ID of this note.
#Artificial Neuron #Neural Network #Basics #Activation Function

$$ \tanh(x) = \frac{\sinh(x)}{\cosh(x)} = \frac{e^{x} - e^{-x}}{e^x + e^{-x}} $$

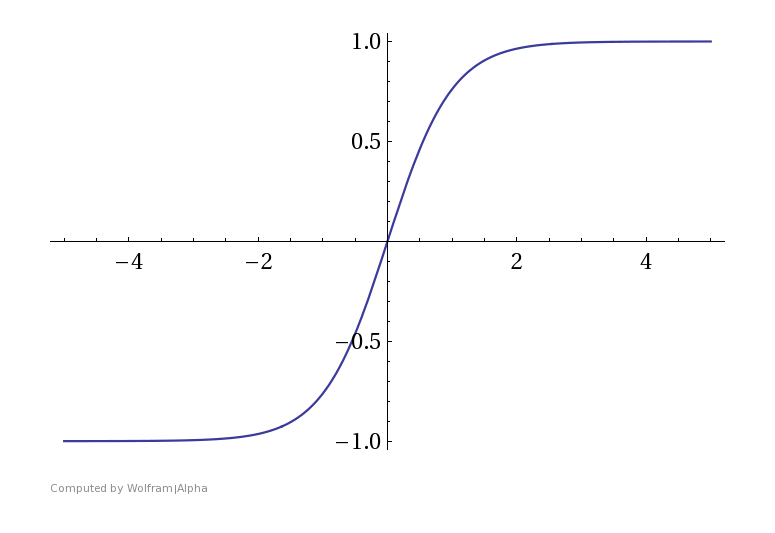
Hyperbolic tangent

Planted: by ;

Similar Articles:
BiPolar Sigmoid
BiPolar sigmoid function and its properties
Conic Section Function
Conic Section Function and its properties
ELU
ELU and its properties
Leaky ReLu
Leaky ReLu and its properties
Links to:
Artificial Neural Networks
Simple artificial neural networks using multilayer perceptron

L Ma (2018). 'Hyperbolic Tanh', Datumorphism, 11 April. Available at: https://datumorphism.leima.is/cards/machine-learning/neural-networks/activation-hyperbolic-tangent/.