Centered Kernel Alignment (CKA)

GROWING This note is being developed. It is readible but changes are being applied.
cards/machine-learning/measurement/centered-kernel-alignment.md Current Note ID: The unique ID of this note.
#Data #Representation #Similarity

Centered Kernel Alignment (CKA) is a similarity metric designed to measure the similarity of between representations of features in neural networks1.

Definition of CKA

CKA is based on the [[Hilbert-Schmidt Independence Criterion (HSIC)]] Hilbert-Schmidt Independence Criterion (HSIC) Given two kernels of the feature representations $K=k(x,x)$ and $L=l(y,y)$, HSIC is defined as12 $$ \operatorname{HSIC}(K, L) = \frac{1}{(n-1)^2} \operatorname{tr}( K H L H ), $$ where $x$, $y$ are the representations of features, $n$ is the dimension of the representation of the features, $H$ is the so-called [[centering matrix]] Centering Matrix Useful when centering a vector around its mean . We can choose different kernel functions $k$ and $l$. For example, if $k$ and $l$ are linear kernels, … .

Hilbert-Schmidt Independence Criterion (HSIC)

Given two kernels of the feature representations $K=k(x,x)$ and $L=l(y,y)$, HSIC is defined as

$$ \operatorname{HSIC}(K, L) = \frac{1}{(n-1)^2} \operatorname{tr}( K H L H ), $$

where

  • $x$, $y$ are the representations of features,
  • $n$ is the dimension of the representation of the features,
  • $H$ is the so-called .
We can choose different kernel functions $k$ and $l$. For example, if $k$ and $l$ are linear kernels, we have $k(x, y) = l(x, y) = x \cdot y$. In this linear case, HSIC is simply …

But HSIC is not invariant to isotropic scaling which is required for a similarity metric of representations1. CKA is a normalization of HSIC,

$$ \operatorname{CKA}(K,L) = \frac{\operatorname{HSIC}(K, L)}{\sqrt{\operatorname{HSIC}(K,K) \operatorname{HSIC}(L,L)}}. $$

Applications

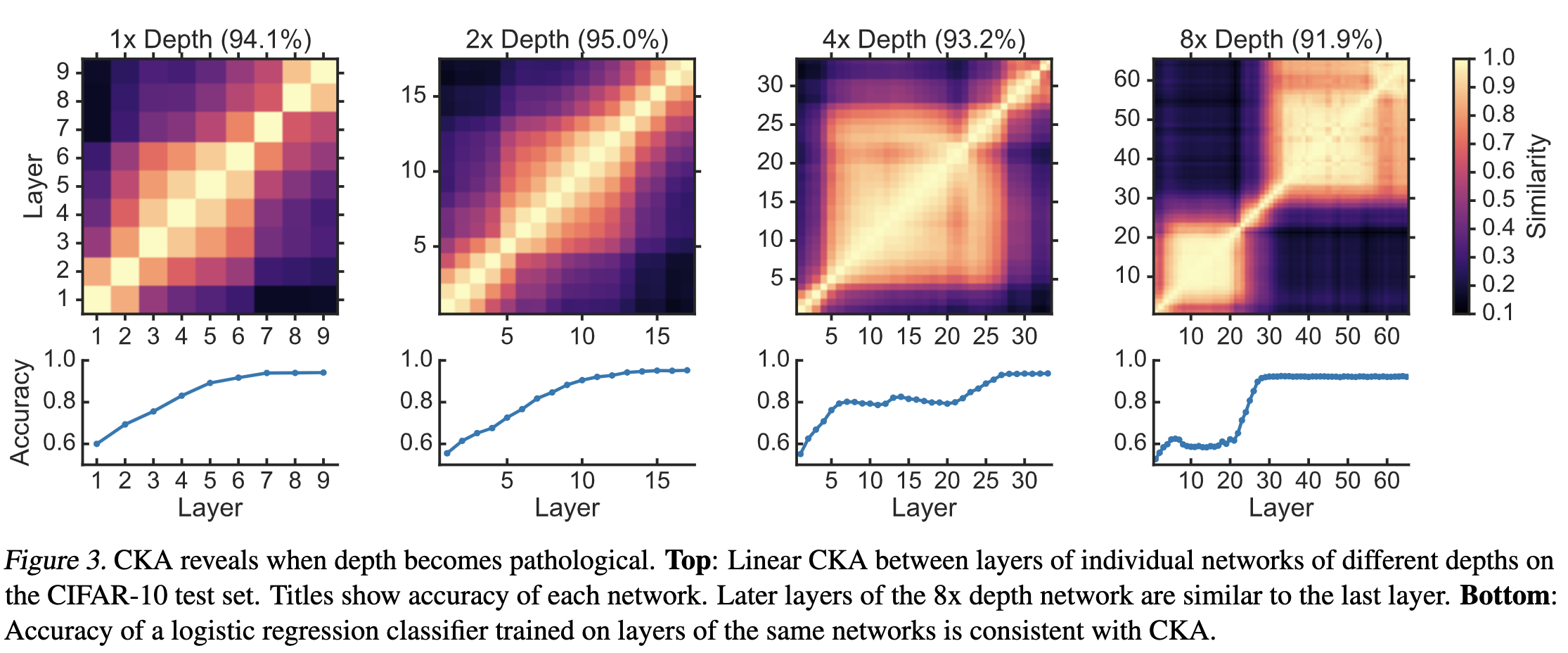
Kornblith2019

Kornblith2019

CKA has Problems too

Seita et al argues that CKA is a metric based on intuitive tests, i.e., calculate cases that we believe that should be similar and check if the CKA values is consistent with this intuition2. Seita et al built a quantitive benchmark2.

  1. Kornblith S, Norouzi M, Lee H, Hinton G. Similarity of Neural Network Representations Revisited. arXiv [cs.LG]. 2019. Available: http://arxiv.org/abs/1905.00414 ↩︎ ↩︎

  2. Seita D. How should we compare neural network representations? In: The Berkeley Artificial Intelligence Research Blog [Internet]. [cited 8 Nov 2021]. Available: https://bair.berkeley.edu/blog/2021/11/05/similarity/ ↩︎ ↩︎

Planted: by ;

Similar Articles:
Hilbert-Schmidt Independence Criterion (HSIC)
Given two kernels of the feature representations $K=k(x,x)$ and $L=l(y,y)$, HSIC is defined as12 $$ …
Alignment and Uniformity
A good representation should be able to separate different instances and cluster similar instances.
ERM: Empirical Risk Minimization
In a [[learning problem]] The Learning Problem The learning problem proposed by Vapnik:1 Given a …
SRM: Structural Risk Minimization
[[ERM]] ERM: Empirical Risk Minimization In a [[learning problem]] The Learning Problem The learning …
cards/machine-learning/measurement/centered-kernel-alignment Links to:
Centering Matrix
Useful when centering a vector around its mean
Hilbert-Schmidt Independence Criterion (HSIC)
Given two kernels of the feature representations $K=k(x,x)$ and $L=l(y,y)$, HSIC is defined as12 $$ …

L Ma (2021). 'Centered Kernel Alignment (CKA)', Datumorphism, 11 April. Available at: https://datumorphism.leima.is/cards/machine-learning/measurement/centered-kernel-alignment/.