Mutual Information
Mutual information is defined as
$$ I(X;Y) = \mathbb E_{p_{XY}} \ln \frac{P_{XY}}{P_X P_Y}. $$
In the case that $X$ and $Y$ are independent variables, we have $P_{XY} = P_X P_Y$, thus $I(X;Y) = 0$. This makes sense as there would be no “mutual” information if the two variables are independent of each other.
Entropy and Cross Entropy
Mutual information is closely related to entropy. A simple decomposition shows that
$$ I(X;Y) = H(X) - H(X\mid Y), $$
which is the reduction of uncertainty in $X$ after observing $Y$.
KL Divergence
This definition of mutual information is equivalent to the following [[KL Divergence]] KL Divergence Kullback–Leibler divergence indicates the differences between two distributions ,
$$ D_{\mathrm{KL}} \left( P_{XY}(x,y) \parallel P_X(x) P_{Y}(y) \right). $$
Conditional Mutual Information
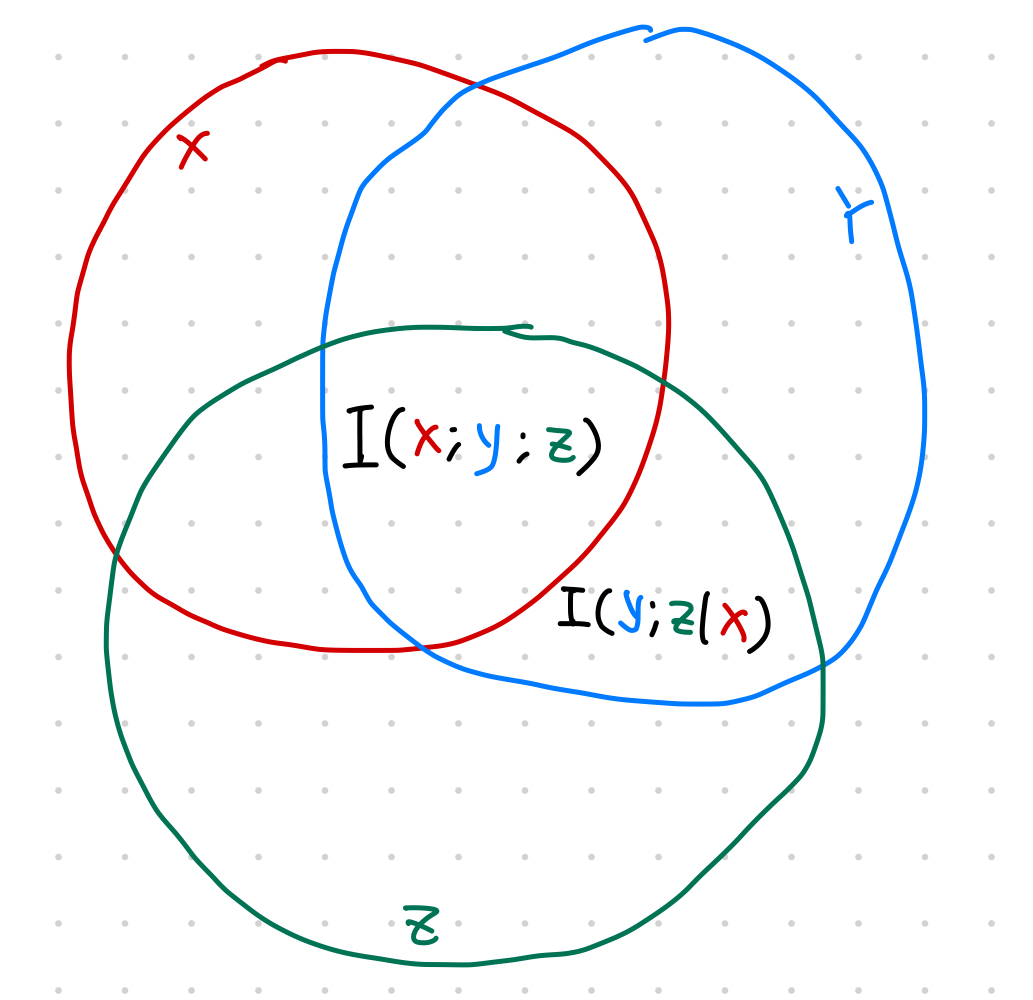
Redraw from wikipedia
cards/information/mutual-information:cards/information/mutual-information Links to:Lei Ma (2021). 'Mutual Information', Datumorphism, 08 April. Available at: https://datumorphism.leima.is/cards/information/mutual-information/.