Fisher Information
Given a probability density model $f(X; \theta)$ for a observable $X$, the amount of information that $X$ carriers regarding the model is called Fisher information.
Given ${\theta}$, the probability of observing the value $X$, i.e., the likelihood is
$$ f(X\mid\theta). $$
To describe the suitability of a model and the observables, we can use a the likelihood $f(X\mid \theta)$. One particular interesting property is the sensitivity of the likelihood in terms of the parameter $\theta$ change. For example, the case on the left is less compatible as we have a large variance in the parameters. The model is not very sensitive to the parameter change.
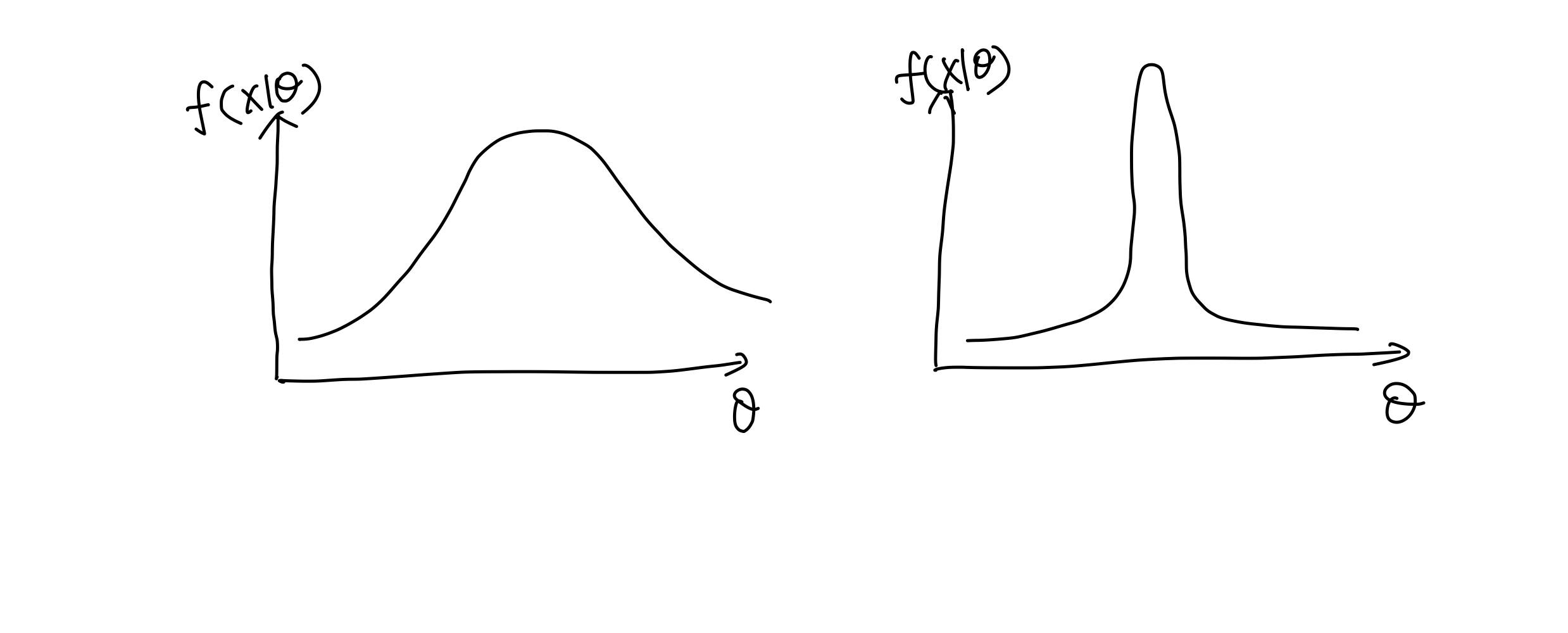
Two scenarios of likelihood.
To describe this sensitivity, we grab the derivative of the log likelihood and define a score function
$$ S(\theta) = \partial_\theta \ln f(X\mid \theta) = \frac{ \partial_\theta f(X\mid \theta) }{\ln f(X\mid\theta)}. $$
The expectation of the squared score function,
$$ I(\theta) = \mathbb E_f [\partial_\theta \ln f(X\mid \theta) ] = \int \left(\partial_\theta \ln f(X\mid\theta)) \right)^2 f(X\mid\theta) ,\mathrm dX. $$
is the Fisher Information.
Under some conditions, we can prove that it is the same as
$$ I(\theta) = \mathbb E_f [\partial^2_\theta \ln f(X\mid \theta) ] = \int f(X\mid\theta) \partial^2_\theta \ln f(X\mid\theta)) ,\mathrm dX. $$
For Bernoulli probability, we have the likelihood
$$ f(X\mid \theta) = \theta^X (1-\theta)^X, $$
where $X$ indicates side of the coin in a coin flip and $\theta$ is the probability of the coin showing head $X=1$. The Fisher information of the Bernulli model is
$$ \begin{align} I_X(\theta) =& \mathbb E _f \left[ \partial^2_\theta \theta^X (1-\theta)^X \right] \\ =& \mathbb E _f \left[ \frac{X}{\theta^2} + \frac{1-X}{(1-\theta)^2} \right] \\ =& \frac{1}{\theta(1-\theta)}. \end{align} $$

Fisher information for Bernoulli model. From Ly et al 2017.
cards/information/fisher-information:cards/information/fisher-information Links to:Lei Ma (2021). 'Fisher Information', Datumorphism, 05 April. Available at: https://datumorphism.leima.is/cards/information/fisher-information/.