Coding Theory Concepts

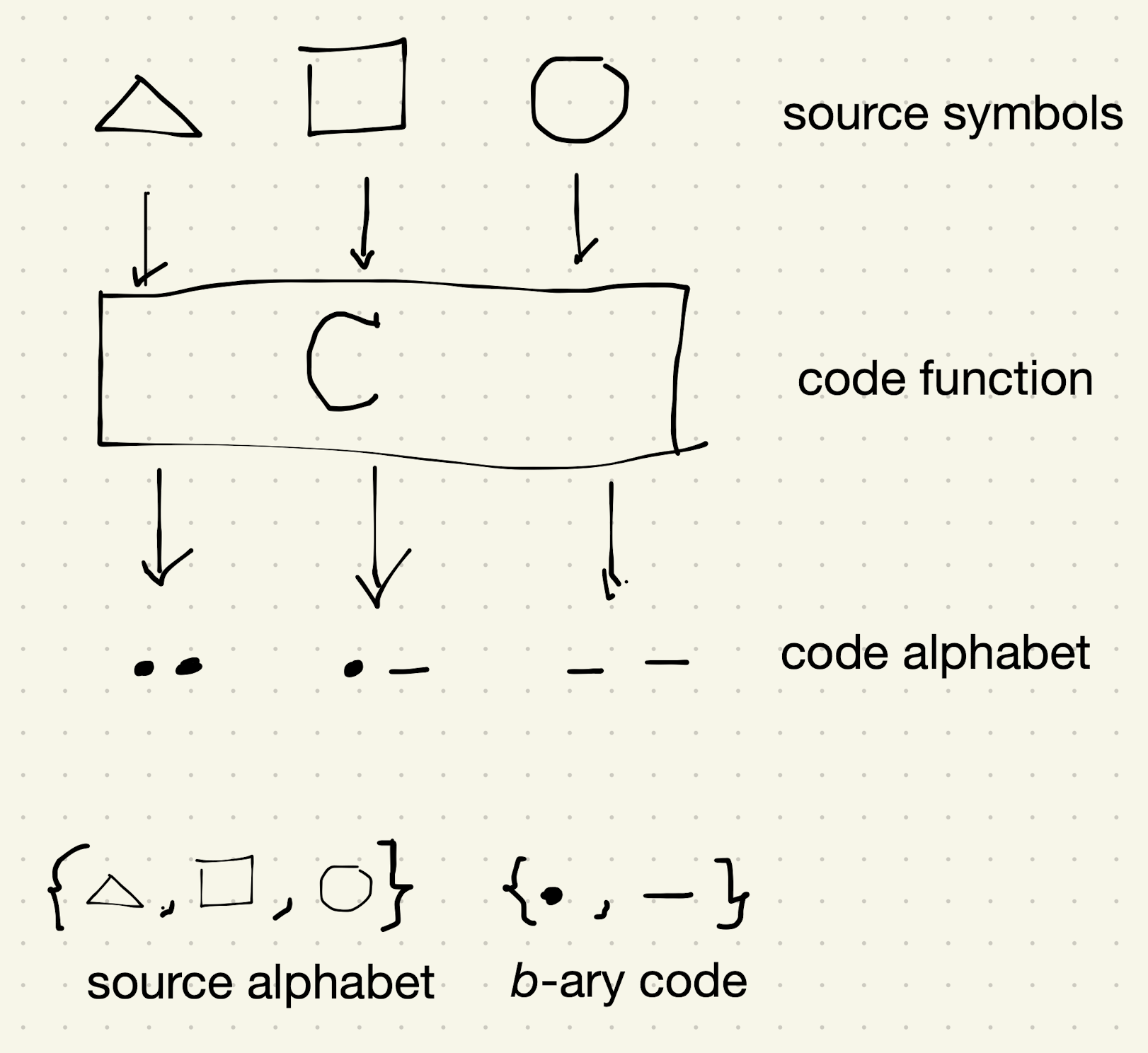
The code function produces code words. The expected length of the code word is limited by the entropy from the source probability $p$.

The Shannon information content, aka self-information, is described by

$$ - \log_2 p(x=a), $$

for the case that $x=a$.

The Shannon entropy is the expected information content for the whole sequence with probability distribution $p(x)$,

$$ \mathcal H = - \sum_x p(x\in X) \log_2 p(x). $$

The Shannon source coding theorem says that for $N$ samples from the source, we can roughly compress it into $N\mathcal H$.