Weisfeiler-Lehman Kernel

GROWING This note is being developed. It is readible but changes are being applied.
cards/graph/graph-weisfeiler-lehman-kernel.md Current Note ID: The unique ID of this note.
#Graph #Statistics

The Weisfeiler-Lehman kernel is an iterative integration of neighborhood information.

We initialize the labels for each node using its own node degree. At each step, we take the neighboring node degrees to form a [[multiset]] Multiset, mset or bag A bag is a set in which duplicate elements are allowed. An ordered bag is a list that we use in programming. . At step $K$, we have the multisets for each node. Those multisets at each node can be processed to form an representation of the graph which is in turn used to calculate statistics of the graph.

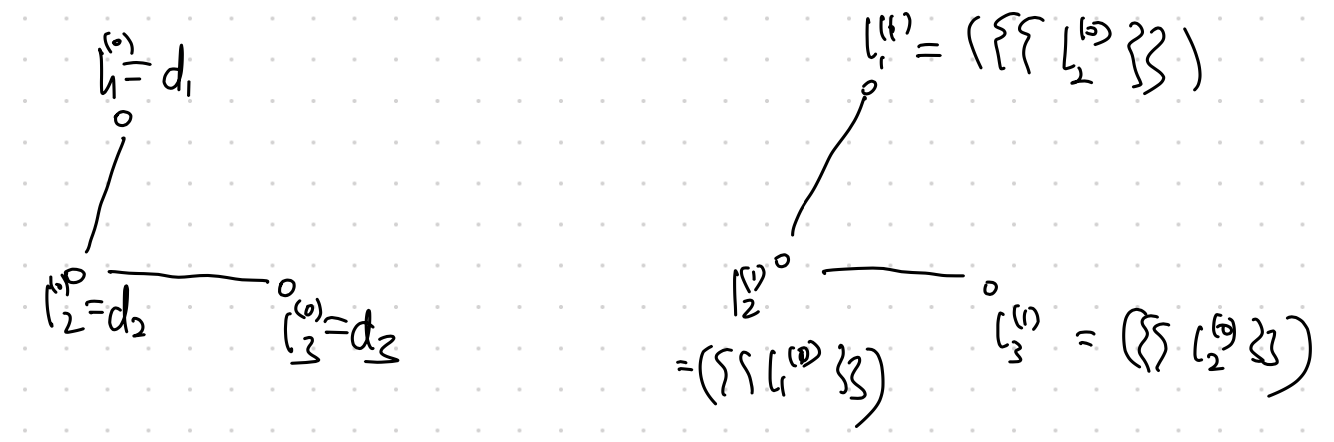
Iterate $k$ steps

Iterate $k$ steps

This iteration can be used to test if two graphs are isomorphism1.

  1. Shervashidze2011 Shervashidze N, Schweitzer P, van Leeuwen EJ, Mehlhorn K, Borgwardt KM. Weisfeiler-Lehman Graph Kernels. J Mach Learn Res. 2011;12: 2539–2561. Available: https://dl.acm.org/doi/10.5555/1953048.2078187  ↩︎

Planted: by ;

References:
  1. Shervashidze2011 Shervashidze N, Schweitzer P, van Leeuwen EJ, Mehlhorn K, Borgwardt KM. Weisfeiler-Lehman Graph Kernels. J Mach Learn Res. 2011;12: 2539–2561. Available: https://dl.acm.org/doi/10.5555/1953048.2078187
  2. Hamilton2020 Hamilton WL. Graph Representation Learning. Morgan & Claypool Publishers; 2020. pp. 1–159. doi:10.2200/S01045ED1V01Y202009AIM046
Dynamic Backlinks to cards/graph/graph-weisfeiler-lehman-kernel:
Weisfeiler-Lehman Kernel
The Weisfeiler-Lehman kernel is an iterative integration of neighborhood information. We initialize …
Graph Isomorphism
For two graphs, $\mathcal G$ and $\mathcal H$, the two graphs are isomorphism on the following …
cards/graph/graph-weisfeiler-lehman-kernel Links to:
What is Graph
Graph A graph $\mathcal G$ has nodes $\mathcal V$ and edges $\mathcal E$, $$ \mathcal G = ( \mathcal …
Additional Double Backet Links:
Multiset, mset or bag
A bag is a set in which duplicate elements are allowed. An ordered bag is a list that we use in …

L Ma (2021). 'Weisfeiler-Lehman Kernel', Datumorphism, 09 April. Available at: https://datumorphism.leima.is/cards/graph/graph-weisfeiler-lehman-kernel/.