Betweenness Centrality of a Graph
Betweenness centrality of a node $v$ is measurement of how likely the shortest path between two nodes $u_s$ and $u_t$ is gonna pass through node $v$,
$$ c(v) = \sum_{v\neq u_s\neq u_t} \frac{\sigma_{u_su_t}(v) }{\sigma_{u_su_t}}, $$
where $\sigma_{u_su_t}(v)$ is the number of shortest path between $u_s$ and $u_t$, and passing through $u$, while $\sigma_{u_su_t}$ is the number of shortest path between $u_s$ and $u_t$.
A figure from wikipedia demonstrates this idea well. The nodes on the outreach have smaller betweenness centrality, while the nodes in the core have higher betweenness centrality.
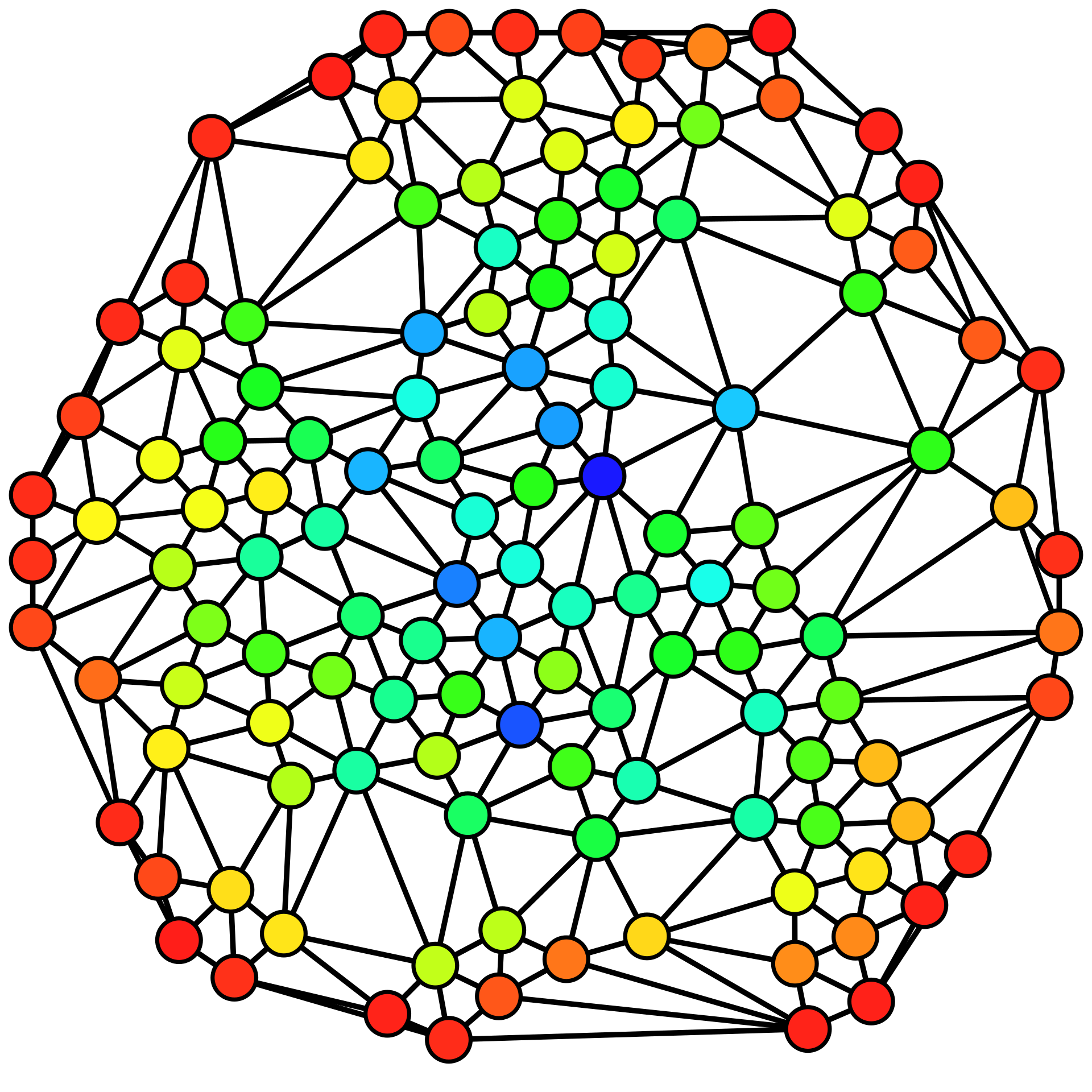
Source: Wikipedia
cards/graph/graph-betweenness-centrality:cards/graph/graph-betweenness-centrality Links to:L Ma (2021). 'Betweenness Centrality of a Graph', Datumorphism, 09 April. Available at: https://datumorphism.leima.is/cards/graph/graph-betweenness-centrality/.