Curriculum

GROWING This note is being developed. It is readible but changes are being applied.
awesome/curriculum/index.md Current Note ID: The unique ID of this note.
#roadmap #career

Prerequisites

Programming

alternatives:

  • R
  • Matlab

Python

Some essential libraries:

Use virtual environments:

Use notebooks

Computer Science

These theories make people think faster. They don’t pose direct limits on what data scientists can do but they will definitely give data scientists a boost.

Math

Some basic understanding of these is absolutely required. Higher levels of these topics will also be listed in details.

Engineering for Data Scientist

I use the book by Adreas Kretz as a checklist 1.

[[Data Engineering for Data Scientists: Checklist]] Data Engineering for Data Scientists: Checklist A checklist to get a shallow understanding of the basics and the ecosystem

Data Storage and Retrieval

Statistics

Descriptive statistics

It is crucial for the interpretations in statistics.

  • Probability theory
  • Summary statistics
    • location
    • variation
    • correlation
      • [[Covariance Matrix]] Covariance Matrix Also known as the second central moment is a measurement of the spread.
      • [[Explained Variation]] Explained Variation Using [[Fraser information]] Fraser Information The Fraser information is $$ I_F(\theta) = \int g(X) \ln f(X;\theta) , \mathrm d X. $$ When comparing two models, $\theta_0$ and $\theta_1$, the information gain is $$ \propto (F(\theta_1) - F(\theta_0)). $$ The Fraser information is closed related to [[Fisher information]] Fisher Information Fisher information measures the second moment of the model sensitivity with respect to the parameters. , Shannon information, and [[Kullback information]] KL …
      • [[Correlation Coefficient and Covariance for Numeric Data]] Correlation Coefficient and Covariance for Numeric Data Detecting correlations using correlations for numeric data
  • Laws
    • Law of large numbers
    • Central limit theorem
    • Law of total variance
    • much more
  • Probability Estimation
    • Kernel density estimation

Inferential statistics

To get closer to the ultimate question about causality

EDA

Data wrangling and exploratory data analysis.

Understand the Source of the data

  • Know the source
  • Understand the data collection procedure
  • Understand the limitation of the data

Dimensionality and Numerosity Reduction

Reduce the dimension of the data:

  • PCA
    • [[Unsupervised Learning: PCA]] Unsupervised Learning: PCA Principal component analysis is a method to remove redundancies of the features by looking into the variances.
  • SparsePCA
  • ICA

Numerosity reduction:

  • Parametric
    • Using model parameters to represent the data
  • Non-parametric
    • Histograms
    • Clustering
    • Resampling

Data Normalization

Normalization is very important in many models.

Normalization of raw data:

Normalization in neural networks:

  • Batch normalization

Missing Data

Data imputation

Unbiased Estimators

Binning

  • Bin the sparse values
  • Bin continuous data if necessary

Outlier Detection

Anomaly Detection

Noisy Data

Sampling and Resampling

Feature Selection

Baseline Model

Association Rules

Visualization

What to show

  • Relationship
  • Composition
    • Compose to compare
    • Compose to calculate (the total)
    • Compose to form a distribution

Types of Charts

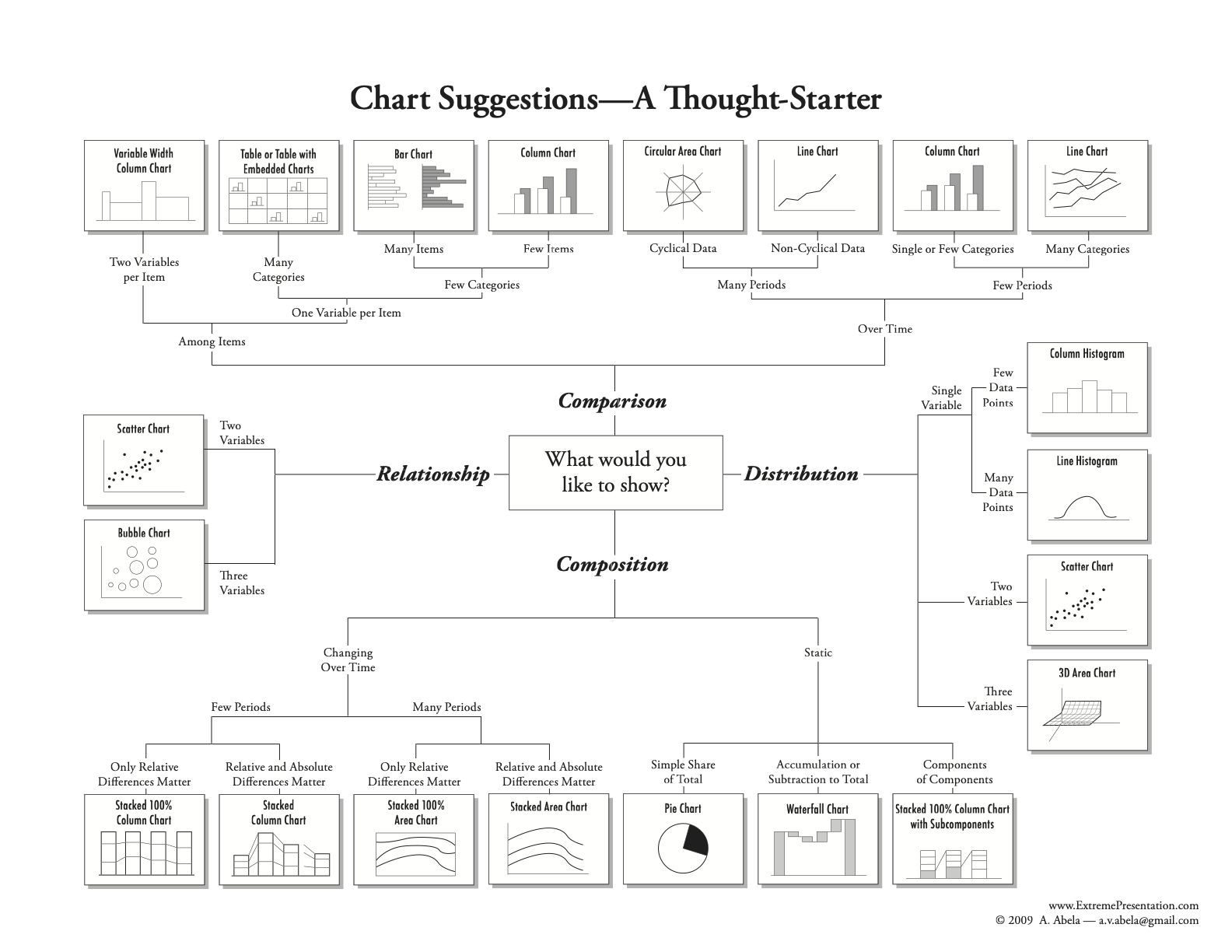
Know your charts. Source: Chart Suggestions — A Thought-Starter

Know your charts. Source: Chart Suggestions — A Thought-Starter

Other useful references:

Grammar of Graphics

  • [[Graph Creation]] Graph Creation Stages Three stages of making a graph: Specification Assembly Display Specification Statistical graphic specifications are expressed in six statements DATA: a set of data operations that create variables from datasets TRANS: variable transformations (e.g., rank) SCALE: scale transformations (e.g., log) COORD: a coordinate system (e.g., polar) ELEMENT: graphs (e.g., points) and their aesthetic attributes (e.g., color) GUIDE: one or more guides (axes, legends, etc.) Assembly Assembling a scene …
  • [[The Grammar of Graphics]] The Grammar of Graphics Reading notes for the book The Grammar of Graphics

Tools

Machine Learning

Concepts

  • Features
  • Estimators
  • Risk
    • [[ERM: Empirical Risk Minimization]] ERM: Empirical Risk Minimization In a [[learning problem]] The Learning Problem The learning problem proposed by Vapnik:1 Given a sample: $\{z_i\}$ in the probability space $Z$; Assuming a probability measure on the probability space $Z$; Assuming a set of functions $Q(z, \alpha)$ (e.g. loss functions), where $\alpha$ is a set of parameters; A risk functional to be minimized by tunning “the handles” $\alpha$, $R(\alpha)$. The risk functional is $$ R(\alpha) = \int Q(z, \alpha) \,\mathrm d F(z). $$ A learning problem …
    • [[SRM: Structural Risk Minimization]] SRM: Structural Risk Minimization [[ERM]] ERM: Empirical Risk Minimization In a [[learning problem]] The Learning Problem The learning problem proposed by Vapnik:1 Given a sample: $\{z_i\}$ in the probability space $Z$; Assuming a probability measure on the probability space $Z$; Assuming a set of functions $Q(z, \alpha)$ (e.g. loss functions), where $\alpha$ is a set of parameters; A risk functional to be minimized by tunning “the handles” $\alpha$, $R(\alpha)$. The risk functional is $$ R(\alpha) = \int Q(z, …
    • [[Cross Validation]] Cross Validation Cross validation is a method to estimate the [[risk]] The Learning Problem The learning problem proposed by Vapnik:1 Given a sample: $\{z_i\}$ in the probability space $Z$; Assuming a probability measure on the probability space $Z$; Assuming a set of functions $Q(z, \alpha)$ (e.g. loss functions), where $\alpha$ is a set of parameters; A risk functional to be minimized by tunning “the handles” $\alpha$, $R(\alpha)$. The risk functional is $$ R(\alpha) = \int Q(z, \alpha) \,\mathrm d …
  • Bias and Variance
  • Overfitting, Underfitting
    • [[Goodness-of-fit]] Goodness-of-fit Does the data agree with the model? Calculate the distance between data and model predictions. Apply Bayesian methods such as likelihood estimation: likelihood of observing the data if we assume the model; the results will be a set of fitting parameters. … Why don’t we always use goodness-of-fit as a measure of the goodness of a model? We may experience overfitting. The model may not be intuitive. This is why we would like to balance it with parsimony using some measures of …
  • Loss
    • Huber Loss
  • Performance
    • Regression
      • R^2
    • Classification
      • F score
      • Precision
      • Recall

Frameworks

Supervised

Regression
  • Linear Regression
  • Polynomial Regression
  • Generalized Linear Model
    • Poisson Regression: for counts
      • [[Poisson Regression]] Poisson Regression Poisson regression is a generalized linear model for count data. To model a dataset that is generated from a [[Poisson distribution]] Poisson Process , we only need to model the mean $\mu$ as it is the only parameters. The simplest model we can have for some given features $X$ is a linear model. However, for count data, the effects of the predictors are often multiplicative. The next simplest model we can have is $$ \mu = \exp\left(\beta X\right). $$ The $\exp$ makes sure that the mean is …
Classification
  • Logistic Regression
  • SVM
  • Tree
    • [[Decision Tree]] Decision Tree In this article, we will explain how decision trees work and build a tree by hand. The code used in this article can be found in this repo. Definition of the problem We will decide whether one should go to work today. In this demo project, we consider the following features. feature possible values health 0: feeling bad, 1: feeling good weather 0: bad weather, 1: good weather holiday 1: holiday, 0: not holiday For more compact notations, we use the abstract notation $\{0,1\}^3$ to describe a set …
  • Naive Bayes
  • kNN
  • Gaussian Mixture

Unsupervised

Semi-supervised

Reinforcement Learning

Graphs and Networks

Neural Networks

  1. Kretz2019 The Data Engineering Cookbook  ↩︎

Planted: by ;

L Ma (0001). 'Curriculum', Datumorphism, 01 April. Available at: https://datumorphism.leima.is/awesome/curriculum/.

Table of Contents

Current Note ID:

  • awesome/curriculum/index.md

Links to: